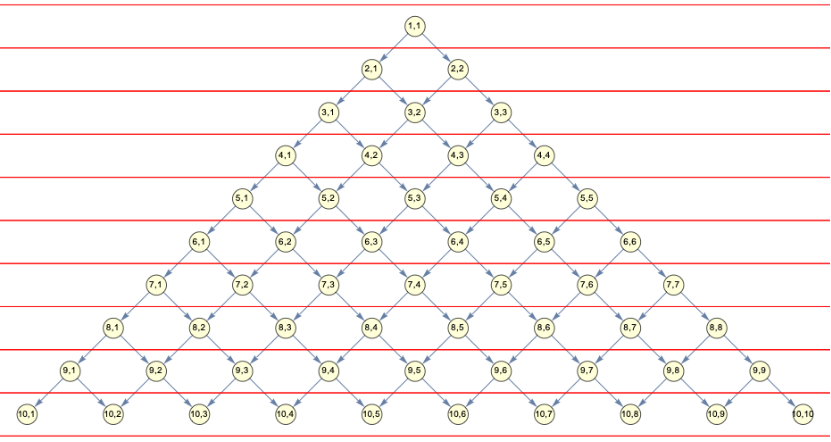
DirectedGraph[Flatten[Table[{v[{i,j}]v[{i+1,j}],v[{i,j}]v[{i+1,j+1}]},{i,10},{j,i}]],VertexCoordinatesCatenate[Table[v[{i,j}]({2(#2-#1/2),-#1}&@@{i,j}),{i,11},{j,i}]],VertexLabelsAutomatic,AspectRatioAutomatic]
In[]:=
Out[]=
regularCausalGraphPlot[layerCount_:9,lineDensity_:1,tan_:0.3,transform_:(#&)]:=DirectedGraph[Flatten[Table[{v[{i,j}]v[{i+1,j}],v[{i,j}]v[{i+1,j+1}]},{i,layerCount-1},{j,i}]],VertexCoordinatesCatenate[Table[v[{i,j}]transform[{2(#2-#1/2),-#1}&@@{i,j}],{i,11},{j,i}]],VertexLabels{x_Placed[Row[Riffle[First[x],","]],Center]},VertexSize.33,VertexStyleLightYellow,AspectRatioAutomatic,Epilog{Style[Table[Line[transform/@{{-100,k-100tan},{100,k+100tan}}],{k,-100.5,100.5,1/lineDensity}],Red]}]
In[]:=
ArcTan[1.]/°
In[]:=
45.
Out[]=
regularCausalGraphPlot[10,1,0,lorentz[0.]]
In[]:=
Out[]=
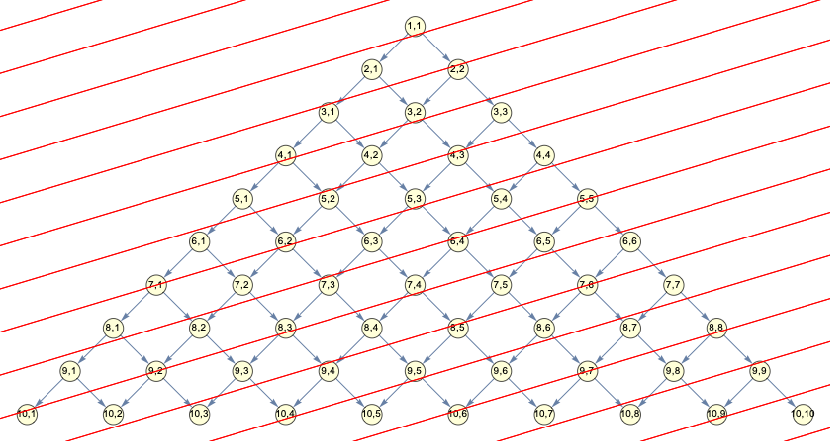
regularCausalGraphPlot[10,1,0.3,lorentz[0.]]
In[]:=
Out[]=
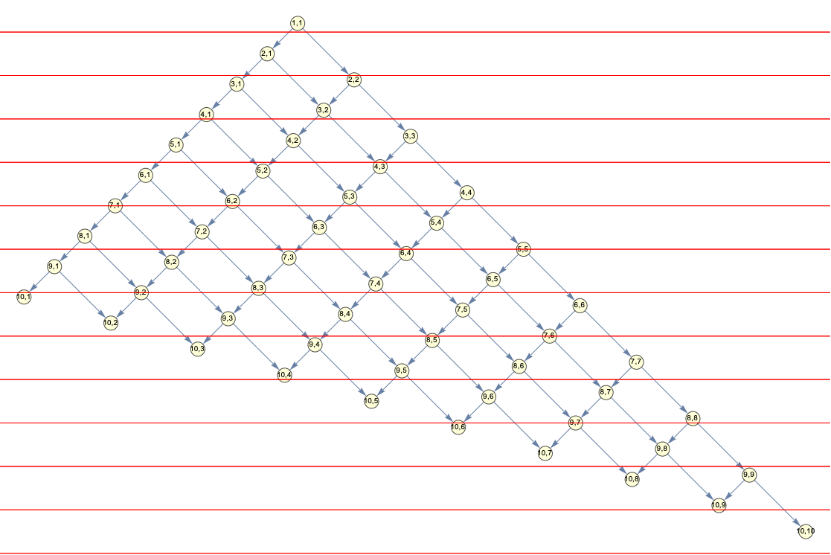
regularCausalGraphPlot[10,1,0.3,lorentz[0.3]]
In[]:=
Out[]=
DirectedGraph[Flatten[Table[{v[{i,j}]v[{i+1,j}],v[{i,j}]v[{i+1,j+1}]},{i,10},{j,i}]],VertexCoordinatesCatenate[Table[v[{i,j}]({2(#2-#1/2),-#1}&@@{i,j}),{i,11},{j,i}]],VertexLabels{x_Placed[Row[Riffle[First[x],","]],Center]},VertexSize.33,VertexStyleLightYellow,AspectRatioAutomatic,Epilog{Style[Table[Line[{{-20,k-12},{20,k}}],{k,6.5,-8.5,-1}],Red]}]
In[]:=
Out[]=
RotationMatrix[Iθ]
In[]:=
{{Cosh[θ],-Sinh[θ]},{Sinh[θ],Cosh[θ]}}
Out[]=
{t,x}{t-vx/c^2,x-vt}
In[]:=
{t,x}t-,-tv+x
vx
2
c
Out[]=
Normalize with γ
{t,x}{t-βx,-tβ+x}
In[]:=
{t,x}{t-xβ,x-tβ}
Out[]=
trans[f_,n_:10]:=DirectedGraph[Flatten[Table[{v[{i,j}]v[{i+1,j}],v[{i,j}]v[{i+1,j+1}]},{i,n},{j,i}]],VertexCoordinatesCatenate[Table[v[{i,j}]f[{2(#2-#1/2),-#1}&@@{i,j}],{i,11},{j,i}]],VertexLabelsAutomatic,Epilog{Table[Line[f/@{{-20,k-12},{0,k-6},{20,k}}],{k,6.5,-8.5,-1}]}]
In[]:=
lorentz[β_][{t_,x_}]:={t-βx,-tβ+x}/Sqrt[1-β^2]
In[]:=
trans[lorentz[.3],10]
In[]:=
Manipulate[trans[lorentz[b],8],{b,0,1}]
In[]:=
In a string substitution system, we could have a foliation based on the string
In a string substitution system, we could have a foliation based on the string
WM analog
WM analog
toState[str_]:=Riffle[MapIndexed[Table[#2[[1]],#/.{"A"1,"B"2}]&,Characters[str]],Partition[Range[StringLength[str]],2,1]]
In[]:=
WolframModel[{{1},{1,2},{2,2}}{{1,1},{1,2},{2}},toState["AAAABAABBAABBB"],Infinity,"CausalGraph"]
In[]:=
Out[]=
WolframModel[{{1},{1,2},{2,2}}{{1,1},{1,2},{2}},toState["AAAABAABBAABBB"],Infinity,"StatesPlotsList"]
In[]:=
Out[]=
RulePlot[WolframModel[{{1},{1,2},{2,2}}{{1,1},{1,2},{2}}]]
In[]:=
Out[]=
toState[str_]:=MapThread[If[#"B",Append[#2,Last[#2]],#2]&,{Characters[str],Partition[Range[StringLength[str]+1],2,1]}]
In[]:=
WolframModel[{{1,2,2},{2,3}}{{1,2},{2,3,3}},toState["BBBAABBAABAAAA"],Infinity,"CausalGraph"]
In[]:=
Out[]=
RulePlot[WolframModel[{{1,2,2},{2,3}}{{1,2},{2,3,3}}]]
In[]:=
Out[]=
Minkowski in SS
Minkowski in SS
We can put a Minkowski norm on here....