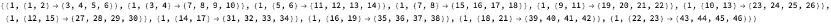[[ https://community.wolfram.com/groups/-/m/t/1729148 ]]
[[ https://community.wolfram.com/groups/-/m/t/1729148 ]]
In[]:=
RulePlot[WolframModel[encodeCARule[110,0]]]
Out[]=
In[]:=
RulePlot[WolframModel[#]]&/@encodeCARule[110,0]
Out[]=
In[]:=
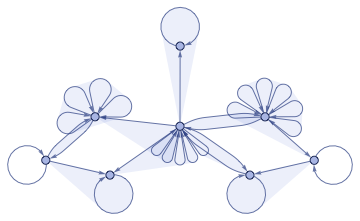
WolframModelPlot[encodeCAState[{1}]]
Out[]=
In[]:=
WolframModelPlot[encodeCAState[{1,1}]]
Out[]=
In[]:=
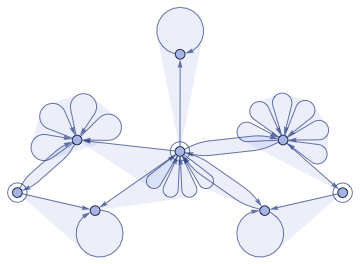
WolframModelPlot[encodeCAState[{1,0,1}]]
Out[]=
In[]:=
WolframModelPlot[encodeCAState[{1,1,0}]]
Out[]=
In[]:=
WolframModelPlot[encodeCAState[{0}]]
Out[]=
In[]:=
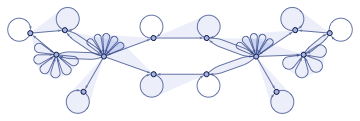
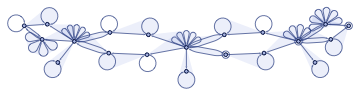
WolframModel[encodeCARule[110,0],encodeCAState[{1}],4]
Out[]=
Turing machine
Turing machine
In[]:=
RulePlot[WolframModel[encodeTMRule[{596440,2,3},0]]]
Out[]=
In[]:=
RulePlot[WolframModel[encodeTMRule[{2506,2,2},0]]]
Out[]=
RulePlot[WolframModel[encodeTMRule[{2506,2,2},0]]]
TuringMachine[
In[]:=
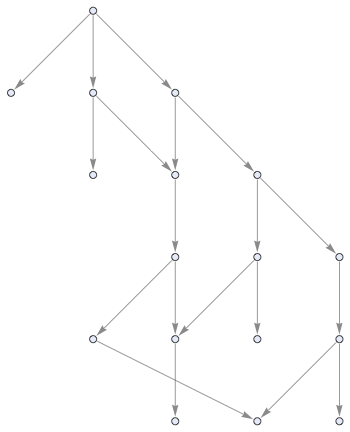
MultiwaySystem[WolframModel[encodeTMRule[{596440,2,3},0]],encodeTMState[{1,1},{0}],5,"StatesGraphStructure"]
Out[]=
In[]:=
MultiwaySystem[WolframModel[encodeTMRule[{596440,2,3},0]],encodeTMState[{1,1},{0}],8,"StatesGraphStructure"]
Out[]=
CA-like picture
CA-like picture
In[]:=
WolframModel[{{x,y},{x,z}}{{x,z},{x,w},{y,w},{z,w}},{{0,0},{0,0}},4,"StatesList"]
Out[]=
< Look for slow growth rules.... >
< Look for slow growth rules.... >
In[]:=
WolframModel[{{x,y},{x,z}}{{x,z},{x,w},{y,w},{z,w}},{{0,0},{0,0}},4,"AllEventsList"]
Out[]=
How far did it need to go to find an edge....