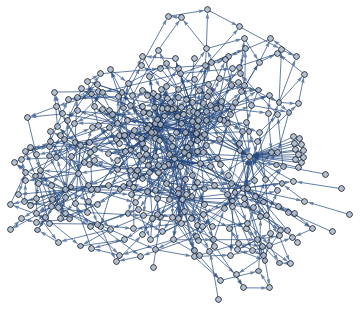
Theorem dependency network for Wolfram commutative axioms (COMPLETE)

In[]:=
fullcax=(Join[AxiomaticTheory["WolframCommutativeAxioms"],{ForAll[a,Square[a]==a·a],ForAll[{a,b},CircleTimes[a,b]==(a·b)·(a·b)],ForAll[{a,b},CirclePlus[a,b]==(a·a)·(b·b)]}]/.{CircleTimesWedge,CirclePlusVee})
Out[]=

∀
{a.,b.,c.}
(a.·b.)·(a.·(b.·c.))a.,
∀
{a.,b.}
a.·b.b.·a.,
∀
a
aa·a,
∀
{a,b}
a⋀b(a·b)·(a·b),
∀
{a,b}
a⋁b(a·a)·(b·b)
In[]:=
notableProofs=FindEquationalProof[#,fullcax]&/@toProve;
In[]:=
notableGraphs=notableProofs[[#]]["ProofGraph"]&/@Range[Length[notableProofs]];
In[]:=
notableDatasets=notableProofs[[#]]["ProofDataset"]&/@Range[Length[notableProofs]];
In[]:=
replaceVertices[g_Integer]:=VertexReplace[notableGraphs[[g]],Thread[VertexList[notableGraphs[[g]]](notableDatasets[[g]][[All,1]][[Values]]//Normal)]]
In[]:=
notableGraphsReplaced=Map[replaceVertices,Range[Length[notableGraphs]]];
Rule
:Pattern x1_ appears on the right-hand side of rule (x1_⋁x1_x1)Tooltip
Substitution Lemma 11
Pattern[2]⋁Pattern[2]x1
.
Rule
:Pattern x1_ appears on the right-hand side of rule (x1_⋁x1_x1)Tooltip
Substitution Lemma 11
Pattern[2]⋁Pattern[2]x1
.
Rule
:Pattern x1_ appears on the right-hand side of rule (x1_⋀x1_x1)Tooltip
Substitution Lemma 10
Pattern[2]⋀Pattern[2]x1
.
General
:Further output of Rule::rhs will be suppressed during this calculation.
In[]:=
dependencyNetwork=Apply[GraphUnion,notableGraphsReplaced]
Out[]=
Axioms are red, lemmas are orange, propositions are yellow, conclusion is purple.
In[]:=
axiomStatements=(Delete[#,0]&/@fullcax)[[2;;;;2]]/.{a.x1,b.x2,c.x3,ax1,bx2,cx3}
Out[]=
{(x1·x2)·(x1·(x2·x3))x1,x1·x2x2·x1,x1x1·x1,x1⋀x2(x1·x2)·(x1·x2),x1⋁x2(x1·x1)·(x2·x2)}
In[]:=
propositions=VertexList[dependencyNetwork,_?(MemberQ[Sort/@toProve,Sort[#]]&)];
In[]:=
conclusion=VertexList[dependencyNetwork,True];
In[]:=
axiomStatements=(Delete[#,0]&/@fullcax)[[2;;;;2]]/.{a.x1,b.x2,c.x3,ax1,bx2,cx3};
In[]:=
axiomsList=VertexList[dependencyNetwork,_?(MemberQ[Sort/@axiomStatements,Sort[#]]&)];
In[]:=
lemmas=Complement[VertexList[dependencyNetwork],VertexList[dependencyNetwork,True],VertexList[dependencyNetwork,_?(MemberQ[Sort/@toProve,Sort[#]]&)],VertexList[dependencyNetwork,_?(MemberQ[Sort/@axiomStatements,Sort[#]]&)]];
In[]:=
Graph[dependencyNetwork,GraphLayout"LayeredDigraphEmbedding",VertexStyle{_?(MemberQ[propositions,#]&)Yellow,_?(MemberQ[axiomsList,#]&)Red,_?(MemberQ[conclusion,#]&)Purple,_?(MemberQ[lemmas,#]&)Orange},VertexSize2]
Out[]=
In[]:=
VertexCount[%]
Out[]=
387
In[]:=
Graph[dependencyNetwork,GraphLayout"LayeredDigraphEmbedding",VertexStyle{_?(MemberQ[propositions,#]&)Yellow,_?(MemberQ[axiomsList,#]&)Red,_?(MemberQ[conclusion,#]&)Purple,_?(MemberQ[lemmas,#]&)Orange},VertexSize2,VertexLabels(#If[MemberQ[propositions,#],Automatic,None]&/@VertexList[dependencyNetwork])]
Out[]=
In[]:=
Graph[%,GraphLayout"SpringElectricalEmbedding"]
Out[]=
Jonathan wrote this following piece of code to show which theorems depend on each other: