In[]:=
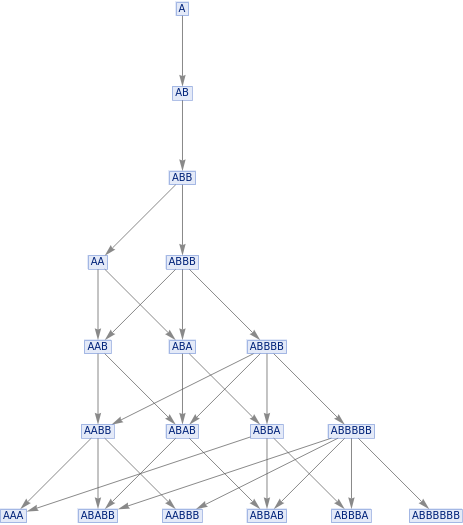
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},"A",6,"StatesGraph"]
Out[]=
In[]:=
FindStringReplacePath[{"A""AB","BB""A"},"A","AAA"]
Out[]=
{A,AB,ABB,AA,AAB,AABB,AAA}
In[]:=
FindStringReplacePath[{"A""AB","BB""A"},"A","AAAAA"]
Out[]=
{A,AB,ABB,AA,AAB,AABB,AAA,AAAB,AAABB,AAAA,AAAAB,AAAABB,AAAAA}
In[]:=
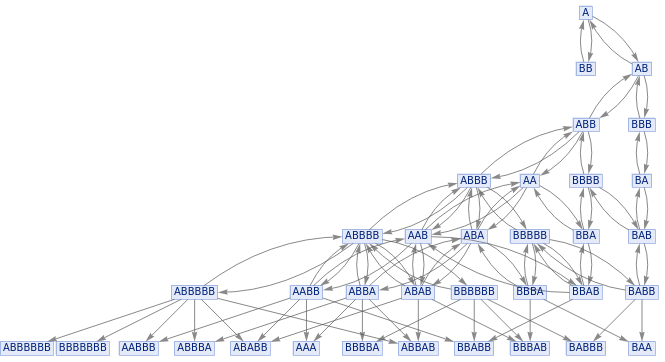
ResourceFunction["MultiwaySystem"][Join[#,Reverse/@#]&[{"A"->"AB","BB""A"}],"A",6,"StatesGraph",GraphLayout"LayeredDigraphEmbedding"]
Out[]=
In[]:=
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A","AB""AA"},"A",6,"StatesGraph"]
Out[]=
In[]:=
FindStringReplacePath[{"A""AB","BB""A"},"A","AAAAA"]
Out[]=
{A,AB,ABB,AA,AAB,AABB,AAA,AAAB,AAABB,AAAA,AAAAB,AAAABB,AAAAA}
In[]:=
FindStringReplacePath[{"A""AB","BB""A","AB""AA"},"A","AAAAA"]
Out[]=
{A,AB,AA,AAB,AAA,AAAB,AAAA,AAAAB,AAAAA}

Did we generate all possible LHSs for our candidate

In[]:=
SimpleGraph[EquationalMultiwaySystem[{{"AB","BA"},{"AAAB","AAAB"}},2,"ProofGraph"],VertexLabels->Automatic,GraphLayout"LayeredDigraphEmbedding",EdgeStyle{DirectedEdge[_,_,1]Gray,DirectedEdge[_,_,2]Dotted}]
Out[]=

Euclid

In[]:=
euc=ResourceData["Theorem Network from Euclid's Elements"];
In[]:=
VertexOutComponent[euc,<|"Book"1,"Theorem"7|>,1]
Out[]=
{Book1,Theorem7,None,Common Notion5,Book1,Theorem5,Postulate1}
In[]:=
VertexOutComponent[euc,<|"Book"1,"Theorem"7|>,2]
Out[]=
{Book1,Theorem7,None,Common Notion5,Book1,Theorem5,Postulate1,Postulate2,Common Notion3,Book1,Theorem3,Book1,Theorem4}
In[]:=
VertexOutComponent[euc,<|"Book"1,"Theorem"7|>,Infinity]
Out[]=
{Book1,Theorem7,None,Common Notion5,Book1,Theorem5,Postulate1,Postulate2,Common Notion3,Book1,Theorem3,Book1,Theorem4,Common Notion1,Book1,Theorem2,Postulate3,Common Notion4,Book1,Theorem1}

Does Euclid only back-reference, and not forward reference?

Does every theorem eventually depend only on postulates and common notions?

Which theorems are most popular, used directly?

In[]:=
TakeLargestBy[VertexList[euc],VertexInDegree[euc,#]&,5]
Out[]=
{Book10,Theorem11,Book6,Theorem1,Book5,Theorem11,Book1,Theorem3,Book10,Theorem6}
In[]:=
VertexInDegree[euc,#]&/@%729
Out[]=
{60,53,47,47,43}
In[]:=
eec[<|"Book"b_,"Theorem"t_|>]:=Entity["GeometricScene",StringTemplate["EuclidBook`b`Proposition`t`"][<|"b"b,"t"t|>]]
In[]:=
eec["Book"1,"Theorem"3]
In[]:=
Euclid book 1 proposition 3
GEOMETRIC SCENE
["Statement"]
Out[]=
To cut off from the longer of two given unequal line segments a part equal to the shorter.
In[]:=
Euclid book 1 proposition 3
GEOMETRIC SCENE
["Scene"]
Out[]=
GeometricScene[{{A.,B.,C.,D.,E.,F.},{}},{{Line[{A.,B.}],Line[{C.,D.}],EuclideanDistance[A.,B.]>EuclideanDistance[C.,D.]},{Line[{A.,E.}],EuclideanDistance[A.,E.]EuclideanDistance[C.,D.]},{GeometricAssertion[{CircleThrough[{E.},A.],Line[{A.,B.}]},{Concurrent,F.}]}},{EuclideanDistance[A.,F.]EuclideanDistance[C.,D.]}]

Direct uses

Did Euclid only Back Reference

[[[ Something is wrong with the following;; only picking ]]]]

Decompose into purely the action of axioms

Source bug:

Number of axioms needed for each proof: [[[ WRONG! ]]]

Shortening of 17gon construction: https://mathworld.wolfram.com/Heptadecagon.html

Communities of theorems