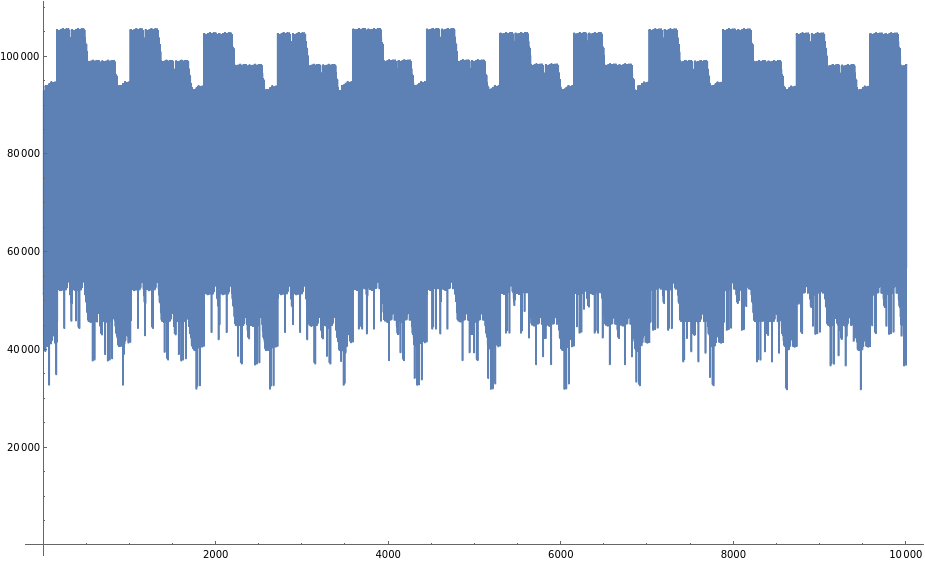
Size 10^8
Size 10^8
In[]:=
<<CombinatorEvolve`
In[]:=
rr8=SKCombinatorLeftmostOutermostLeafCounts[s[s[s]][s][s][s][s[s][k[k]]],10^8];
In[]:=
Length[rr8]
Out[]=
100000001
In[]:=
First/@Split[FoldList[Min,Drop[rr8,10^6]]]
Out[]=
{14968,14638,14621,14555,14554,14222,14179,14110,14042,14021,13231,13188,12988,12971,12927,12925,12857,12855,12815,12790,12773,12732,12476,12459,12352,11216,11132,8269,8160,8158,5830,5699,5659,5101,5017,4634,4525,4523,4163,3778,3761,3400,3168,3059,3057,2697,2472,2451,2149,2148,1972,1955,1888,1837,1797,1439,1395,1172,1103,1101,901,676,659,458,346,277,275,75,27}
In[]:=
Position[rr8,27]
Out[]=
{{34339093}}
In[]:=
Position[rr8,75]
Out[]=
{{34339092}}
In[]:=
First/@Split[FoldList[Max,Drop[rr8,34339093]]]
Out[]=
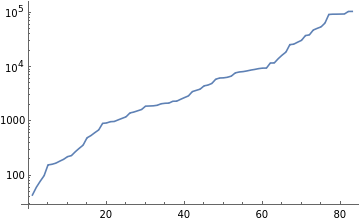
{44,61,79,100,158,162,170,185,200,224,234,276,319,365,498,547,620,696,919,934,986,996,1066,1137,1211,1428,1484,1567,1653,1906,1919,1933,1978,2108,2154,2169,2345,2355,2549,2744,2942,3531,3722,3918,4501,4657,4987,5972,6285,6328,6484,6814,7799,8112,8242,8486,8799,9041,9354,9554,9569,11877,11887,14213,16540,18870,25855,26386,28711,31039,38018,39037,48017,51528,54892,64422,93007,94034,94124,94481,94836,105568,105723}
In[]:=
ListLinePlot[%,ScalingFunctions"Log"]
Out[]=
In[]:=
First/@Split[FoldList[Max,rr8]]
Out[]=
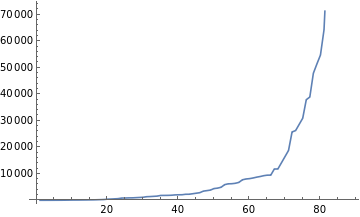
{10,11,14,17,20,24,32,49,66,92,96,104,119,134,158,168,210,253,299,432,481,554,630,853,868,920,930,1000,1071,1145,1362,1418,1501,1587,1840,1853,1867,1912,2042,2088,2103,2279,2289,2483,2678,2876,3465,3656,3852,4435,4591,4921,5906,6219,6262,6418,6748,7733,8046,8176,8420,8733,8975,9288,9488,9503,11811,11821,14147,16474,18804,25789,26320,28645,30973,37952,38971,47951,51462,54826,64356,92941,93968,94058,94415,94770,105502,105657,105723}
In[]:=
ListLinePlot[%]
Out[]=
In[]:=
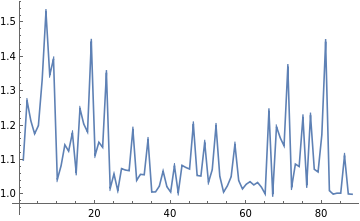
ListLinePlot[Ratios[%7]]
Out[]=
In[]:=
Max[rr8]
Out[]=
105723
In[]:=
Position[rr8,Max[rr8]]
Out[]=
{{36536622}}
In[]:=
Position[rr8,105657]
Out[]=
{{2197536},{38969617},{45749918},{47280991},{47472631}}
In[]:=
Flatten[%]
Out[]=
{2197536,38969617,45749918,47280991,47472631}
In[]:=
Differences[%]
Out[]=
{36772081,6780301,1531073,191640}
In[]:=
BlockMap[Median,rr8,1000];
In[]:=
ListStepPlot[%]
Out[]=
In[]:=
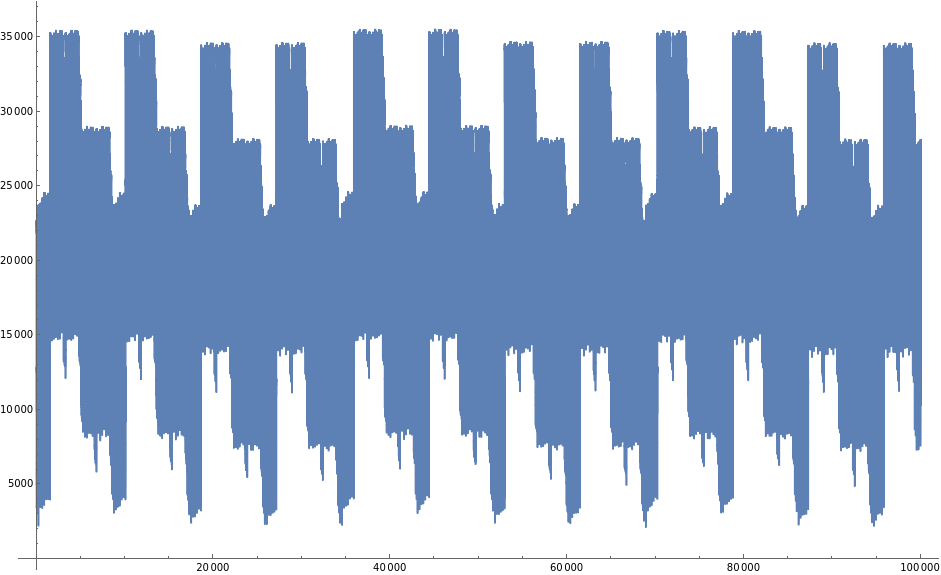
BlockMap[Max,rr8,10000];
In[]:=
ListStepPlot[%]
Out[]=
Getting running mins
Getting running mins
Size 10^9 ?
Size 10^9 ?