In[]:=
LayeredGraphPlot[SubstitutionSystemCausalGraph[{"A""AB","BB""BB"},"A",15],VertexLabelsAutomatic]
Out[]=
In[]:=
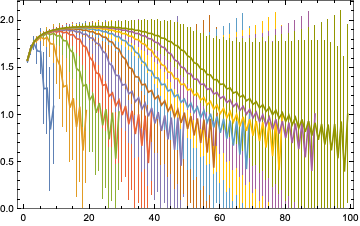
ListLinePlot[Table[LogDifferences@RaggedMeanAround[Values[GraphNeighborhoodVolumes[SubstitutionSystemCausalGraph[{"A""AB","BB""BB"},"A",t]]]],{t,10,100,10}],FrameTrue,PlotRange{0,Automatic}]
Out[]=
In[]:=
ListLinePlot[LogDifferences[{1,2,4,7,12,17,24,31,40,50,61,74,88,104,121,140,160,182,204,228,251,276,300,326,351,377,403,429,455,481,507,533,559,584,608,630,651,670,688,704,719,732,743,753,762,769,775,779,782}]]
Out[]=
In[]:=
RaggedMeanAround[%]
Out[]=
{1,2.78
±
0.15
,5.50±
0.22
,8.0±
0.7
,10.5±
0.5
}Transpose
Extract[
In[]:=
%[1]
Out[]=
{1,3,6,10,15,21,28,36,44,51,57,62,66,69,71}
In[]:=
Differences[%]
Out[]=
{2,3,4,5,6,7,8,8,7,6,5,4,3,2}
In[]:=
Differences[%]
Out[]=
{1,1,1,1,1,1,0,-1,-1,-1,-1,-1,-1}
In[]:=
GraphNeighborhoodVolumes[SubstitutionSystemCausalGraph[{"A""AB","BB""BB"},"A",30],{1}]
Out[]=
1{1,3,6,10,15,21,28,36,45,55,66,78,91,105,120,136,151,165,178,190,201,211,220,228,235,241,246,250,253,255}
In[]:=
ListLinePlot[LogDifferences[%[1]]]
Out[]=
In[]:=
GraphNeighborhoodVolumes[SubstitutionSystemCausalGraph[{"AA""AAA"},"AA",20],{1}][1]
Out[]=
{1,3,6,11,19,32,51,80,124,189,286,430,643,942,1391,2016,2727,3793,5392,5393}
In[]:=
Ratios[%]//N
Out[]=
{3.,2.,1.83333,1.72727,1.68421,1.59375,1.56863,1.55,1.52419,1.51323,1.5035,1.49535,1.46501,1.47665,1.44932,1.35268,1.39091,1.42157,1.00019}
In[]:=
ListLinePlot[%]
Out[]=
In[]:=
ListLinePlot[LogDifferences[%9]]
Out[]=
In[]:=
GraphNeighborhoodVolumes[SubstitutionSystemCausalGraph[{"A""AA","A""AA","AAA""A"},"AA",20],{1}][1]
Out[]=
{1,3,5,7,11,14,17,23,27,31,39,45,51,63,71,79,95,106,117,139,154,169,199,219,239,279,306,333,387,423,459,531,579,627,723,787,851,979,1065,1151,1323,1438,1553,1783,1937,2091,2399,2605,2811,3223,3498,3773,4323,4690,5057,5791,6281,6771,7751,8405}
In[]:=
ListLinePlot[LogDifferences[%13]]
Out[]=
WM cases
WM cases
12 steps
400 steps
Standard 2,4 rule
Standard 2,4 rule