In[]:=
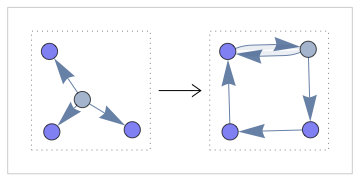
RulePlot[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}}]]
Out[]=
In[]:=
GraphPlot[Rule@@@WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],20,"FinalState"]]
Out[]=
In[]:=
GraphPlot[Rule@@@#]&/@WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],20,"StatesList"]
Out[]=
In[]:=
rr30=Graph[Rule@@@WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],30,"FinalState"]]
Out[]=
In[]:=
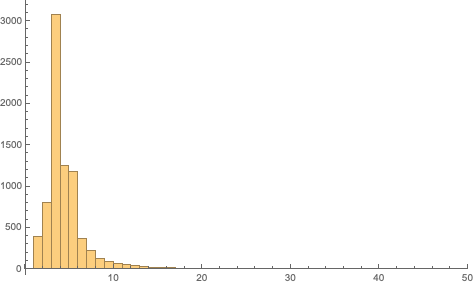
Histogram[VertexDegree[rr30]]
Out[]=
In[]:=
Max[VertexDegree[rr30]]
Out[]=
48
In[]:=
Histogram[VertexDegree[rr30],PlotRangeAll]
Out[]=
In[]:=
GraphPlot[%357]
Out[]=
Vertex Degree Growth
Vertex Degree Growth
Random Evolution
Random Evolution
Difference Patterns
Difference Patterns
(( Like two intersecting light cones ))
Causal-cone-informed graph layout ??
Dimension Computation
Dimension Computation