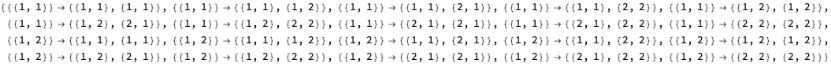Binary Edges, Multiple Transformations
Binary Edges, Multiple Transformations
WolframModelExplorer1R[Table[RandomWolframModelRuleMulti[{{{{1,2}}{{2,2}},3},{{{2,2}}{{1,2}},2}}],30],4]
In[]:=
EnumerateWolframModelRules[{{1,2}}{{2,2}},2]
Out[]=
In[]:=
EnumerateWolframModelRules[{{2,2}}{{1,2}},2]
Out[]=
In[]:=
Outer[List,EnumerateWolframModelRules[{{1,2}}{{2,2}},2],EnumerateWolframModelRules[{{2,2}}{{1,2}},2],1]
Out[]=
In[]:=
Catenate[%]
Out[]=
In[]:=
WolframModelExplorer1[%226,{{0,0},{0,0}},4]
(Nothing interesting)
In[]:=
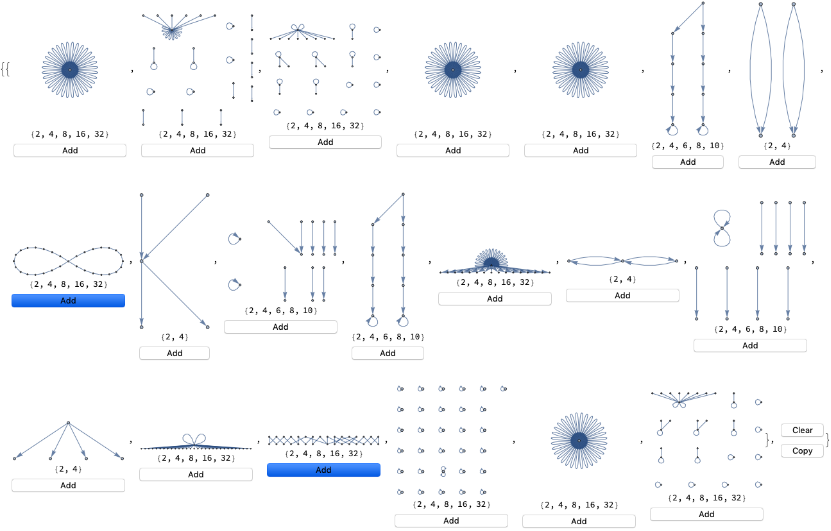
WolframModelExplorer1Binary[Table[First@RandomWolframModelRuleMulti[{{{{1,2}}{{2,2}},3},{{{2,2}}{{1,2}},2}}],10],{{0,0},{0,0}},4]
Out[]=
In[]:=
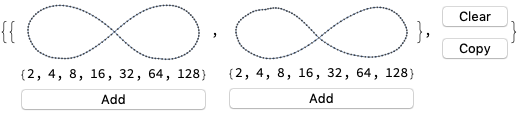
WolframModelExplorer1Binary[Table[First@RandomWolframModelRuleMulti[{{{{1,2}}{{2,2}},3},{{{2,2}}{{1,2}},2}}],20],{{0,0},{0,0}},4]
Out[]=
{{{{1,2}}{{1,3},{3,2}},{{1,1},{2,1}}{{1,1}}},{{{1,2}}{{3,1},{3,2}},{{1,1},{2,1}}{{2,1}}}}
In[]:=
WolframModelExplorer1Binary[{{{{1,2}}{{1,3},{3,2}},{{1,1},{2,1}}{{1,1}}},{{{1,2}}{{3,1},{3,2}},{{1,1},{2,1}}{{2,1}}}},{{0,0},{0,0}},6]
Out[]=
In[]:=
WolframModelExplorer1Binary[{{{{1,2}}{{1,3},{3,2}},{{1,1},{2,1}}{{1,1}}},{{{1,2}}{{3,1},{3,2}},{{1,1},{2,1}}{{2,1}}}},{{0,0}},6]
Out[]=
In[]:=
WolframModelExplorer1Binary[{{{{1,2}}{{1,3},{3,2}}},{{{1,2}}{{3,1},{3,2}},{{1,1},{2,1}}{{2,1}}}},{{0,0},{0,0}},6]
Out[]=
In[]:=
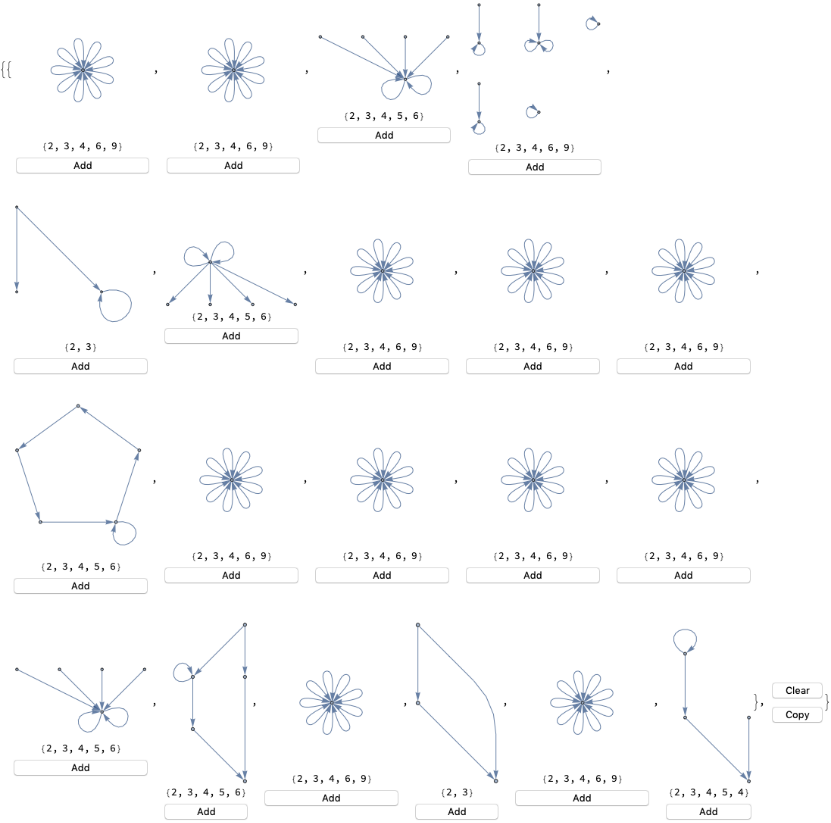
WolframModelExplorer1Binary[Table[First@RandomWolframModelRuleMulti[{{{{2,2}}{{3,2}},3},{{{2,2}}{{1,2}},2}}],20],{{0,0},{0,0}},4]
Out[]=
