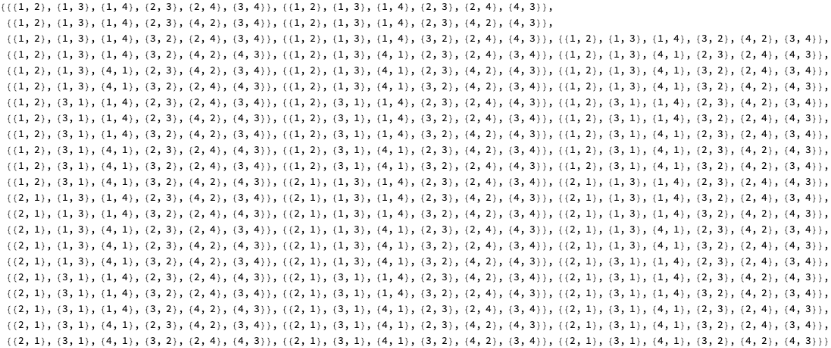NOTE: Problems with PlanarGraphQ

From GraphData

GraphData["Planar"]
In[]:=
Out[]=
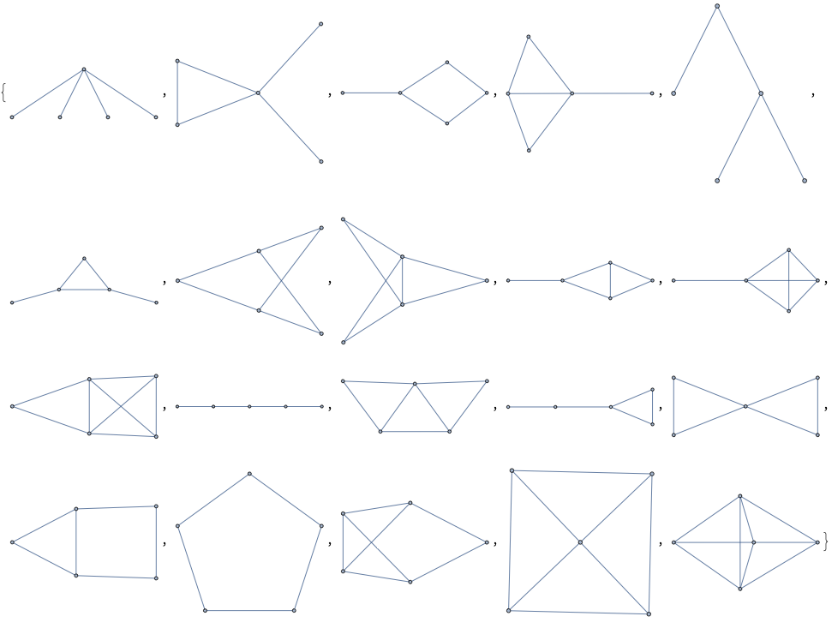
GraphData/@Take[%,6]
In[]:=
Out[]=

From “House of Graphs”

Import["https://hog.grinvin.org/data/planar/planar_graphs/planar_conn.5.g6"]
In[]:=
Out[]=
GetPlanarGraphs[n_Integer]:=Import[StringTemplate["https://hog.grinvin.org/data/planar/planar_graphs/planar_conn.``.g6"][n]]
In[]:=
GetPlanarGraphs[2]
In[]:=
Out[]=
GetPlanarGraphs[3]
In[]:=

,

Out[]=
GetPlanarGraphs[4]
In[]:=
Out[]=
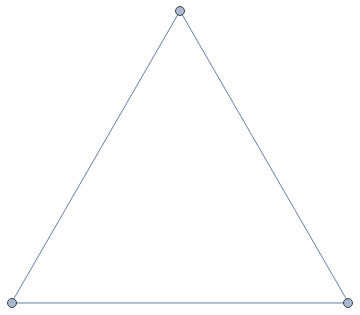
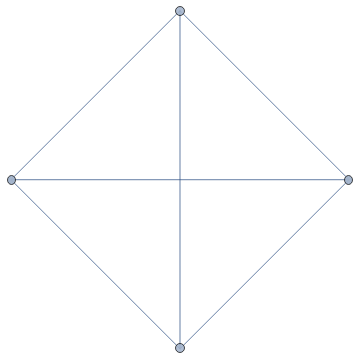
EdgeList

In[]:=
{12,13,14,23,24,34}
Out[]=
AllReversals[g_Graph]:=With[{e=List@@@EdgeList[g]},MapThread[Construct,{#,e}]&/@Tuples[{Identity,Reverse},Length[e]]]
In[]:=
AllReversals

In[]:=
Out[]=
(Should also check termination; check there was an update)
WolframModel[{{x,y}}{{x,z},{y,z},{z,z}},#,1,"FinalState"]&/@%23
In[]:=
Out[]=
PlanarGraphQ[UndirectedEdge@@@#]&/@%
In[]:=
{False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False}
Out[]=

Testing Code

$GraphList=DeleteDuplicates[ParallelMapMonitored[FindCanonicalHypergraph,Catenate[AllReversals/@Catenate[Table[If[Head[#]=!=List,{#},#]&@GetPlanarGraphs[i],{i,2,5}]]]]];
In[]:=
Length[$GraphList]
In[]:=
563
Out[]=
Export["/Users/sw/Dropbox/Physics/Data/PlanarGraph.wxf",$GraphList];
In[]:=
$GraphList=Import["/Users/sw/Dropbox/Physics/Data/PlanarGraph.wxf"];
In[]:=
$RandomGraphList=(SeedRandom[563];RandomSample[$GraphList,25]);
In[]:=
RuleOnGraph[rule_,graph_]:=Graph[UndirectedEdge@@@WolframModel[rule,List@@@EdgeList[graph],1,"FinalState"]]
In[]:=
RuleOnGraphDirected[rule_,graph_]:=Graph[Rule@@@WolframModel[rule,List@@@EdgeList[graph],1,"FinalState"]]
In[]:=
Working around a PlanarGraphQ crash bug:
xPlanarGraphQ[g_]:=AllTrue[WeaklyConnectedGraphComponents[g],If[VertexCount[#]<5,True,PlanarGraphQ[#]]&]
In[]:=
PlanarTest[rule_,t_Integer:1]:=LengthWhile[$RandomGraphList,xPlanarGraphQ[Graph[UndirectedEdge@@@WolframModel[rule,#,t,"FinalState"]]]&]Length[$RandomGraphList]
In[]:=
PlanarConnectedTest[rule_,t_Integer:1]:=LengthWhile[$RandomGraphList,((WeaklyConnectedGraphQ[#]&&xPlanarGraphQ[#])&@Graph[UndirectedEdge@@@WolframModel[rule,#,t,"FinalState"]])&]Length[$RandomGraphList]
In[]:=
DistributeDefinitions[PlanarTest,$RandomGraphList]
In[]:=
{}
Out[]=
With[{ru=EnumerateWolframModelRules[{{1,2}}{{2,2}}]},Pick[ru,ParallelMapMonitored[PlanarTest[#]&,ru]]]
In[]:=
Out[]=
Length[%149]
In[]:=
73
Out[]=
Graph[Rule@@@#,ImageSizeTiny]&/@$RandomGraphList
In[]:=
Out[]=
(Function[g,RuleOnGraph[#,g]]/@$RandomGraphList)&/@Take[%166,3]
In[]:=
Out[]=
%166[[3]]
In[]:=
{{1,2}}{{3,1},{1,2}}
Out[]=
Graph[Rule@@@RandomChoice[$GraphList]]
In[]:=
Out[]=
RuleOnGraph[%166[[3]],%]
In[]:=
Out[]=
PlanarGraphQ[%]
In[]:=
True
Out[]=
NestListRuleOnGraph[{{1,2}}{{3,1},{1,2}},#]&,
,4
In[]:=
Out[]=
PlanarGraphQ/@%
In[]:=
{True,True,True,True,True}
Out[]=
With[{ru=EnumerateWolframModelRules[{{1,2}}{{2,2}}]},Pick[ru,ParallelMapMonitored[PlanarTest[#,2]&,ru]]]
In[]:=
Out[]=
Length[%]
In[]:=
73
Out[]=
With[{ru=EnumerateWolframModelRules[{{1,2}}{{2,2}}]},Pick[ru,ParallelMapMonitored[PlanarTest[#,3]&,ru]]]
In[]:=
Out[]=
With[{ru=EnumerateWolframModelRules[{{1,2}}{{2,2}}]},Pick[ru,ParallelMapMonitored[PlanarTest[#,4]&,ru]]]
In[]:=
Out[]=
Length[%]
In[]:=
73
Out[]=
Length[EnumerateWolframModelRules[{{1,2}}{{2,2}}]]
In[]:=
73
Out[]=
NestListRuleOnGraph[{{x,y}}{{x,y},{y,z},{z,x}},#]&,
,4
In[]:=
Out[]=
PlanarGraphQ/@%
In[]:=
{True,True,True,True,True}
Out[]=
PlanarGraph

In[]:=
Out[]=
PlanarGraph

In[]:=
Out[]=
NestListRuleOnGraph[{{x,y}}{{x,z},{x,z},{z,y}},#]&,
,4
In[]:=
Out[]=
PlanarGraphQ/@%
In[]:=
{True,True,True,True,True}
Out[]=
PlanarGraph[Rule@@@#]&/@WolframModel[{{x,y}}{{x,y},{y,z},{z,x}},{{1,1}},5,"StatesList"]
In[]:=
Out[]=
PlanarGraph[Rule@@@#,ImageSizeTiny]&/@WolframModel[{{x,y}}{{x,y},{y,z},{z,x}},{{1,2}},5,"StatesList"]
In[]:=
Out[]=
PlanarTest[{{x,y},{z,y}}{{u,v},{v,y},{y,u},{u,x},{v,z}}]
In[]:=
True
Out[]=
NestListRuleOnGraph[{{x,y},{z,y}}{{u,v},{v,y},{y,u},{u,x},{v,z}},#]&,
,4
In[]:=
Out[]=
PlanarGraph/@%
In[]:=
PlanarGraph
:
is not a planar graph.
PlanarGraph
:
is not a planar graph.
PlanarGraph
:
is not a planar graph.
General
:Further output of PlanarGraph::nplanar will be suppressed during this calculation.
Out[]=
PlanarTest[{{x,y},{y,z}}{{w,y},{y,z},{z,w},{x,w}}]
In[]:=
False
Out[]=
PlanarTest[{{x,y},{z,y}}{{u,v},{v,y},{y,u},{u,x},{v,z}},2]
In[]:=
False
Out[]=

2,2  3,2 rules

EnumerateWolframModelRules[{{2,2}}{{3,2}}]//Length
In[]:=
4702
Out[]=
$PhysicsDataDirectory
In[]:=
/Users/sw/Dropbox/Physics/Data
Out[]=
allrules=Import["/Users/sw/Dropbox/Physics/Data/RuleEnumerations/22-32c.wxf"];
In[]:=
With[{ru=allrules},Pick[ru,ParallelMapMonitored[PlanarTest[#,1]&,ru]]]
In[]:=
Out[]=
Length[%]
In[]:=
4680
Out[]=
With[{ru=allrules},Pick[ru,ParallelMapMonitored[PlanarTest[#,3]&,ru]]]
In[]:=
Out[]=
Length[%]
In[]:=
4648
Out[]=
​
NestListRuleOnGraph[{{1,2},{3,2}}{{4,5},{5,6},{6,1}},#]&,
,4
In[]:=
Out[]=
RandomSample[%166,5]
In[]:=
Out[]=
Functionr,NestListRuleOnGraph[r,#]&,
,4/@%
In[]:=
Out[]=
With[{ru=allrules},Pick[ru,ParallelMapMonitored[PlanarConnectedTest[#,3]&,ru]]]
In[]:=
Out[]=
Select%172,!IsomorphicGraphQUndirectedGraphRuleOnGraph#,
,UndirectedGraph
&
In[]:=
Out[]=
RandomSample[%,5]
In[]:=
Out[]=
Functionr,Graph[#,GraphLayout"SpringElectricalEmbedding"]&/@NestListRuleOnGraphDirected[r,#]&,
,6/@%179
In[]:=
Out[]=
Map[PlanarGraph[UndirectedGraph[#]]&,%190,{2}]
In[]:=
Out[]=
{{1,2},{2,3}}{{1,3},{3,4},{2,3}}
Length[%]
In[]:=
135
Out[]=
With[{ru=%%},Pick[ru,ParallelMapMonitored[PlanarTest[#,2]&,ru]]]
In[]:=
Out[]=
With[{ru=%},Pick[ru,ParallelMapMonitored[PlanarTest[#,3]&,ru]]]
In[]:=
{}
Out[]=
RulePlot[WolframModel[#]]&/@%%
In[]:=
Out[]=

1,2  3,2

allrules=Import["/Users/sw/Dropbox/Physics/Data/RuleEnumerations/12-32c.wxf"];
In[]:=
Length[allrules]
In[]:=
506
Out[]=
With[{ru=allrules},Pick[ru,ParallelMapMonitored[PlanarTest[#,1]&,ru]]]
In[]:=
Out[]=
Length[%]
In[]:=
36
Out[]=
With[{ru=%%},Pick[ru,ParallelMapMonitored[PlanarTest[#,2]&,ru]]]
In[]:=
{}
Out[]=
PlanarTest[{{x,y}}{{x,y},{y,z},{z,x}}]
In[]:=
True
Out[]=
PlanarTest[{{x,y}}{{x,y},{y,z},{z,x}},2]
In[]:=
True
Out[]=
PlanarTest[{{x,y}}{{x,y},{y,z},{z,x}},3]
In[]:=
True
Out[]=
FindCanonicalWolframModel[{{x,y}}{{x,y},{y,z},{z,x}}]
In[]:=
{{1,2}}{{1,2},{2,3},{3,1}}
Out[]=
Position[%,{{1,2}}{{1,2},{2,3},{3,1}}]
In[]:=
{}
Out[]=
Take[allrules,{145,150}]
In[]:=
Out[]=
PlanarTest[#,1]&/@%
In[]:=
{True,True,True,True,True,True}
Out[]=
Position[allrules,%221]
In[]:=
{{149}}
Out[]=
ParallelMapMonitored[PlanarTest[#,1]&,allrules]
In[]:=
Out[]=
%[[149]]
In[]:=
False
Out[]=
allrules[[149]]
In[]:=
{{1,2}}{{1,2},{2,3},{3,1}}
Out[]=
PlanarTest[%,1]
In[]:=
True
Out[]=
Map[PlanarTest[#,1]&,allrules]
In[]:=

1,2  2,2

allrules=Import["/Users/sw/Dropbox/Physics/Data/RuleEnumerations/12-22c.wxf"];
In[]:=
Length[allrules]
In[]:=
73
Out[]=
With[{ru=allrules},Pick[ru,ParallelMapMonitored[PlanarTest[#,1]&,ru]]]
In[]:=
Out[]=
Length[%]
In[]:=
9
Out[]=
With[{ru=%%},Pick[ru,ParallelMapMonitored[PlanarTest[#,2]&,ru]]]
In[]:=
{}
Out[]=