Confluence Testing
Confluence Testing
In a terminating rewriting system, confluence is equivalent to the statement that the multiway graph has at most one vertex with out-degree 0.
The sorting substitution:
In[]:=
Graph[MultiwaySystem[{"AB""BA","BA""AB"},{"AAAABAAAA"},6,"EvolutionGraph"],VertexLabelsAutomatic]
Out[]=
Sequential Elementary Cellular Automata
Sequential Elementary Cellular Automata
In[]:=
CASS[rn_]:=Map[StringJoin,#->ReplacePart[#,2->CellularAutomaton[rn][#][[2]]]&/@Tuples[{1,0},3]/.{1"B",0"A"},{2}]
In[]:=
CASS[30]
Out[]=
{BBBBAB,BBABAA,BABBAB,BAABBA,ABBABB,ABAABA,AABABB,AAAAAA}
In[]:=
RulePlot[SubstitutionSystem[%]]
Out[]=
In[]:=
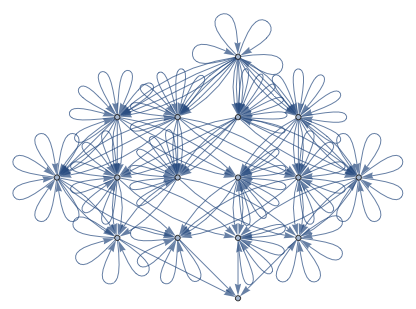
MultiwaySystem[CASS[22],{"AAABAAA"},4,"EvolutionGraph"]
Out[]=
In[]:=
VertexOutDegree[%]
Out[]=
{20,15,15,10,10,10,10,10,5,5,5,5,5,5,5,0,0,0,0,0,0,0}
In[]:=
Table[Count[VertexOutDegree[MultiwaySystem[CASS[n],{"AAABAAA"},4,"EvolutionGraph"]],0],{n,0,255}]
Out[]=
In[]:=
Count[%,0|1]
Out[]=
130
In[]:=
Table[Count[VertexOutDegree[MultiwaySystem[CASS[n],{"AAABAAA"},5,"EvolutionGraph"]],0],{n,0,255}]
Out[]=
In[]:=
Count[%,0|1]
Out[]=
164
In[]:=
Table[Count[VertexOutDegree[MultiwaySystem[CASS[n],{"AAAAABAAAAA"},5,"EvolutionGraph"]],0],{n,0,255}]
Out[]=
In[]:=
Count[%,0|1]
Out[]=
56
In[]:=
MultiwaySystem[CASS[255],{"AAAAABAAAAA"},3,"EvolutionGraph"]
Out[]=
In[]:=
MultiwaySystem[CASS[255],{"AAABAAA"},4,"EvolutionGraph"]
Out[]=
In[]:=
MultiwaySystem[CASS[0],{"AAABAAA"},4,"EvolutionGraph"]
Out[]=
In[]:=
MultiwaySystem[CASS[254],{"AAABAAA"},4,"EvolutionGraph"]
Out[]=
Note that this can’t get to all B’s because of the “open” boundary conditions