Colored Networks
Colored Networks
In[]:=
<<SetReplace`
Approach
Approach
We will think of the colored graphs in terms of vertices, ports and edges. Each vertex is connected to three ports in a specific order, and each edge connects two ports.
We will emulate this with two types of relations:
◼
Vertex-to-port: {vertex, redPort, yellowPort, greenPort}
◼
Edge: {port1, port2}
Since colored graphs are unordered, we will represent each non-hair edge with two edge-relations.
For hairs, we will not specify any port-to-port edges, and just keep the same port on the right-hand side of the rule. That makes it possible to connect hairs to each other.
In[]:=
init={{v1,p1r,p1y,p1g},{v2,p2r,p2y,p2g},{p1r,p2r},{p2r,p1r},{p1y,p2y},{p2y,p1y},{p1g,p2g},{p2g,p1g}};
1
1
In[]:=
evolution1=WolframModel[{{v1,p1r,p1y,p1g},{v2,p2r,p2y,p2g},{p1r,p2r},{p2r,p1r}}{{v3,p1g,p3y,p3g},{v4,p4r,p4y,p1y},{v5,p2g,p5y,p5g},{v6,p6r,p6y,p2y},{p3y,p4r},{p3g,p5g},{p4r,p3y},{p4y,p6y},{p5y,p6r},{p5g,p3g},{p6r,p5y},{p6y,p4y}},init,8]
Out[]=
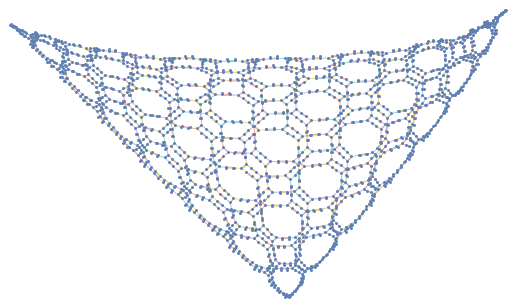
In[]:=
HypergraphPlot[evolution1[-1]]
Out[]=
2
2
In[]:=
evolution2=WolframModel[{{v1,p1r,p1y,p1g},{v2,p2r,p2y,p2g},{p1r,p2r},{p2r,p1r}}{{v3,p1g,p3y,p3g},{v4,p1y,p4y,p4g},{v5,p2g,p5y,p5g},{v6,p2y,p6y,p6g},{p3y,p6g},{p3g,p4y},{p4y,p3g},{p4g,p5y},{p5y,p4g},{p5g,p6y},{p6y,p5g},{p6g,p3y}},init,8]
Out[]=
In[]:=
HypergraphPlot[evolution2[-1]]
Out[]=
3
3
In[]:=
evolution3=WolframModel[{{v1,p1r,p1y,p1g},{v2,p2r,p2y,p2g},{p1r,p2r},{p2r,p1r}}{{v3,p1g,p3y,p3g},{v4,p1y,p4y,p4g},{v5,p2g,p5y,p5g},{v6,p2y,p6y,p6g},{p3y,p5y},{p3g,p4g},{p4y,p6y},{p4g,p3g},{p5y,p3y},{p5g,p6g},{p6y,p4y},{p6g,p5g}},init,8]
Out[]=
In[]:=
HypergraphPlot[evolution3[-1]]
Out[]=
4
4
In[]:=
evolution4=WolframModel[{{v1,p1r,p1y,p1g},{v2,p2r,p2y,p2g},{p1y,p2y},{p2y,p1y}}{{v3,p3r,p1r,p3g},{v4,p4r,p1g,p4g},{v5,p5r,p2r,p5g},{v6,p6r,p2g,p6g},{p3r,p6r},{p3g,p4g},{p4r,p5r},{p4g,p3g},{p5r,p4r},{p5g,p6g},{p6r,p3r},{p6g,p5g}},init,8]
Out[]=
In[]:=
HypergraphPlot[evolution4[-1]]
Out[]=
5
5
In[]:=
evolution5=WolframModel[{{v1,p1r,p1y,p1g},{v2,p2r,p2y,p2g},{p1r,p2r},{p2r,p1r}}{{v3,p1g,p3y,p3g},{v4,p1y,p4y,p4g},{v5,p2g,p5y,p5g},{v6,p2y,p6y,p6g},{p3y,p5y},{p3g,p4y},{p4y,p3g},{p4g,p6g},{p5y,p3y},{p5g,p6y},{p6y,p5g},{p6g,p4g}},init,8]
Out[]=
In[]:=
HypergraphPlot[evolution5[-1]]
Out[]=
6
6
7
7