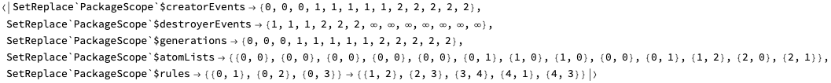WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],20]
In[]:=
Out[]=
%53["EventsCount"]
In[]:=
525
Out[]=
WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],2]//First
In[]:=
Out[]=
WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],3]//First
In[]:=
Out[]=

GenerationEventsCountList

gecl[eo_]:=Differences[eo[[1]][SetReplace`PackageScope`$creatorEvents][[Flatten[Position[Differences[eo[[1]][SetReplace`PackageScope`$generations]],1]]+1]]]
In[]:=
gecl[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],20]]
In[]:=
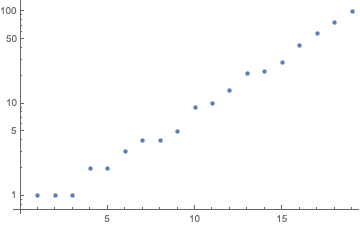
{1,1,1,2,2,3,4,4,5,9,10,14,21,22,28,43,57,75,99}
Out[]=
ListLogPlot[%]
In[]:=
Out[]=
Length/@WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],20]["StatesList"]
In[]:=
{3,5,7,9,13,17,23,31,39,49,67,87,115,157,201,257,343,457,607,805,1053}
Out[]=
Differences[%]
In[]:=
{2,2,2,4,4,6,8,8,10,18,20,28,42,44,56,86,114,150,198,248}
Out[]=
%/2
In[]:=
{1,1,1,2,2,3,4,4,5,9,10,14,21,22,28,43,57,75,99,124}
Out[]=
I.e. net creation of 2 hyperedges per generation

2 rules

{{{{{1,2},{1,3}}{{1,4},{2,4},{4,3},{4,5}},{{1,2},{1,3}}{{1,3}}},{{0,0},{0,0}},9}}
WolframModel[{{{1,2},{1,3}}{{1,4},{2,4},{4,3},{4,5}},{{1,2},{1,3}}{{1,3}}},{{0,0},{0,0}},10]
In[]:=
Out[]=
gecl[%]
In[]:=
{1,2,4,6,9,15,22,34,53}
Out[]=
Differences[Length/@%70["StatesList"]]/2
In[]:=
{1,2,4,6,9,15,22,34,53,79}
Out[]=
With[{eo=WolframModel[#[[1]],#[[2]],10]},{#1,#2,#1-#2}&@@{gecl[eo],Most[Differences[Length/@eo["StatesList"]]/2]}]&/@{{{{{1,2},{2,3}}{{3,2},{4,1},{4,1},{4,3}},{{1,2},{2,1}}{{1,1}}},{{0,0},{0,0}},10},{{{{1,2},{3,2}}{{1,3},{4,2},{4,5},{5,3}},{{1,1},{1,2}}{{2,3}}},{{0,0},{0,0}},12},{{{{1,2},{1,3}}{{2,3},{2,4},{2,5},{4,1}},{{1,1},{1,2}}{{3,3}}},{{0,0},{0,0}},10},{{{{1,2},{2,3}}{{1,4},{3,2},{3,4},{5,2}},{{1,1},{1,1}}{{1,1}}},{{0,0},{0,0}},11},{{{{1,2},{2,3}}{{1,2},{2,4},{4,3},{4,5}},{{1,1},{1,1}}{{1,1}}},{{0,0},{0,0}},9},{{{{1,2},{2,3}}{{2,3},{2,4},{4,1},{5,3}},{{1,2},{2,3}}{{3,3}}},{{0,0},{0,0}},15}}
In[]:=
Out[]=
​
RandomWolframModelRule[{{{{2,2}}{{4,2}},8},{{{2,2}}{{1,2}},3}}]
In[]:=
[◼]
RandomWolframModelRule
[{{{{2,2}}{{4,2}},8},{{{2,2}}{{1,2}},3}}]
Out[]=
Map[(#->With[{eo=Echo@WolframModel[#,{{0,0},{0,0}},10]},{#1,#2,#1-#2}&@@{gecl[eo],Most[Differences[Length/@eo["StatesList"]]/2]}])&,Table[RandomWolframModelRule@@@{{{{2,2}}{{4,2}},8},{{{2,2}}{{1,2}},3}},5]]
In[]:=
WolframModelEvolutionObject
Generations count: 10
Events count: 1023

»
WolframModelEvolutionObject
Generations count: 10
Events count: 1023

»
WolframModelEvolutionObject
Generations count: 10
Events count: 10

»
WolframModelEvolutionObject
Generations count: 1
Events count: 1

»
WolframModelEvolutionObject
Generations count: 1
Events count: 1

»
Out[]=
Framed/@%
In[]:=
Out[]=
Table[RandomWolframModelRule@@@{{{{2,2}}{{4,2}},8},{{{2,2}}{{1,2}},3}},20]
In[]:=
Out[]=
​

Causal Graph

WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],20]["CausalGraph"]
In[]:=
Out[]=
VertexCount[%]
In[]:=
525
Out[]=
WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],10]["CausalGraph"]
In[]:=
Out[]=
VertexCount[%]
In[]:=
32
Out[]=
GraphDistanceMatrix[%92]//MatrixPlot
In[]:=
Out[]=
WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],12]["CausalGraph"]
In[]:=
Out[]=
GraphDistanceMatrix[%]//MatrixPlot
In[]:=
Out[]=
WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],14]["CausalGraph"]
In[]:=
Out[]=
GraphDistanceMatrix[%]//MatrixPlot
In[]:=
Out[]=
WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],14]["CausalGraph"]
In[]:=
Out[]=
LayeredGraphPlot[%100,AspectRatio1/2]
In[]:=
Out[]=
GraphDistanceMatrix[%]//Transpose//MatrixPlot
In[]:=
Out[]=
WolframModel[{{{1,2,2}}{{1,1,3},{3,1,2},{3,1,3},{3,3,3}}},{{0,0,0}},8,"CausalGraph"]
In[]:=
Out[]=
GraphDistanceMatrix[%]//Transpose//MatrixPlot
In[]:=
Out[]=
WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{3,2},{3,4},{4,3},{4,4}},{{0,0},{0,0},{0,0}},21,"CausalGraph"]
In[]:=
Out[]=
GraphDistanceMatrix[%]//Transpose//MatrixPlot
In[]:=
Out[]=
This could be colored by generation.....
Color causal graph by generations .... [ relation to layered graphs?? ]
Graph[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],5]["CausalGraph"],VertexLabelsAutomatic]
In[]:=
Out[]=
For minimal initial conditions, there is always a single first event..... and it’s numbered 1.
cg=WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],5]["CausalGraph"];
In[]:=
Graph[cg,VertexCoordinatesMapIndexed[First[#2]{Automatic,-#1}&,GraphDistance[cg,1]],GraphLayout"SpringElectricalEmbedding",VertexLabelsAutomatic]
In[]:=
Out[]=

DistanceLayeredGraph

DistanceLayeredGraph[g_,root_:1]:=Graph[g,VertexCoordinatesMapIndexed[First[#2]{Automatic,-#1}&,GraphDistance[g,1]],GraphLayout"SpringElectricalEmbedding"]
In[]:=
DistanceLayeredGraph[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],20]["CausalGraph"]]
In[]:=
Out[]=

Generation Layered Graph

eo=WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],3];
In[]:=
eo[[1]]
In[]:=
Out[]=
WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],3]["CausalGraph"]//EdgeList
In[]:=
{12,12,12,13,13,23}
Out[]=
eo[[1]][SetReplace`PackageScope`$generations][[Flatten[Position[Differences[eo[[1]][SetReplace`PackageScope`$creatorEvents]],1]]+1]]
In[]:=
{1,2,3}
Out[]=
LayeredCausalGraph[eo_WolframModelEvolutionObject]:=Graph[eo["CausalGraph"],VertexCoordinatesMapIndexed[First[#2]{Automatic,-#1}&,eo[[1]][SetReplace`PackageScope`$generations][[Flatten[Position[Differences[eo[[1]][SetReplace`PackageScope`$creatorEvents]],1]]+1]]],GraphLayout"SpringElectricalEmbedding"]
In[]:=
LayeredCausalGraph[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],4]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],5]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],6]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],7]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{2,3},{3,4},{4,1},{4,3}},Table[0,3,2],10]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{3,2},{3,4},{4,3},{4,4}},{{0,0},{0,0},{0,0}},10]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{0,1},{0,2},{0,3}}{{1,2},{3,2},{3,4},{4,3},{4,4}},{{0,0},{0,0},{0,0}},15]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{{1,2,2}}{{1,1,3},{3,1,2},{3,1,3},{3,3,3}}},{{0,0,0}},4]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{{1,2,2}}{{1,1,3},{3,1,2},{3,1,3},{3,3,3}}},{{0,0,0}},8]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{{1,2,2}}{{1,1,3},{3,1,2},{3,1,3},{3,3,3}}},{{0,0,0}},11]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{{15,2,3,1},{16,5,6,4},{2,5},{5,2}}{{17,1,8,7},{18,9,10,3},{19,4,12,11},{20,13,14,6},{8,14},{7,9},{9,7},{10,12},{12,10},{11,13},{13,11},{14,8}}},{{1,2,3,4},{5,6,7,8},{2,6},{3,7},{4,8},{6,2},{7,3},{8,4}},8]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{{1,2}}{{1,3},{2,3},{3,3}}},{{1,1}},4]]
In[]:=
Out[]=
TreeGraphQ[%]
In[]:=
True
Out[]=
LayeredCausalGraph[WolframModel[{{{1,2},{1,3},{1,4}}{{2,3},{3,4},{4,5},{5,2},{5,5}}},{{1,1},{1,1},{1,1}},10]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{{1,2},{1,3},{1,4}}{{2,3},{3,4},{4,5},{5,2},{5,5}}},{{1,1},{1,1},{1,1}},12]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{{1,2},{1,3},{1,4}}{{2,3},{3,4},{4,5},{5,2},{5,5}}},{{1,1},{1,1},{1,1}},14]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{{1,2},{1,3},{1,4}}{{2,3},{3,4},{4,5},{5,2},{5,5}}},{{1,1},{1,1},{1,1}},16]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{{1,2},{1,3},{1,4}}{{2,3},{3,4},{4,5},{5,2},{5,5}}},{{1,1},{1,1},{1,1}},20]]
In[]:=
Out[]=
LayeredCausalGraph[WolframModel[{{{1,2},{1,3},{1,4}}{{3,2},{3,4},{3,5},{4,4},{4,5}}},{{1,1},{1,1},{1,1}},12]]
In[]:=
Out[]=
WolframModel[{{{1,2},{1,3},{1,4}}{{3,2},{3,4},{3,5},{4,4},{4,5}}},{{1,1},{1,1},{1,1}},12,"FinalState"]//HypergraphPlot
In[]:=
Out[]=