What is the notion of an integral?
What is the notion of an integral?
Does it still compute area?
d^d x etc.
Vector analysis.... Gauss’s theorem, etc.
What is Div[XXX]?
What is Div[XXX]?
Derivative is just change between graph nodes
Derivative is just change between graph nodes
Divergence is just change of function as a ball expands
Divergence is just change of function as a ball expands
Grad just looks at geodesics to find maximum change
Grad just looks at geodesics to find maximum change
Laplacians / PDEs on graphs...
Laplacians / PDEs on graphs...
Non-Flat Sierpinskis
Non-Flat Sierpinskis
Definitions
Definitions
In[]:=
Vols[graph_,start_:All,max_:Automatic]:=MeanAround/@Transpose[Values[ResourceFunction["GraphNeighborhoodVolumes"][graph,start,max]]]
In[]:=
RandVols[graph_,n_Integer,max_:Automatic]:=Vols[graph,"Random"n,max]
In[]:=
Dims[vols_]:=ListLinePlotTable[(Log[vols[[r+1]]]-Log[vols[[r]]])/(Log[r+1]-Log[r]),{r,Length[vols]-1}],
For Sierpinski
For Sierpinski
In[]:=
HypergraphToGraph[WolframModel[{{1,2,3}}{{1,4,6},{2,5,4},{3,6,5}},{{0,0,0}},5,"FinalState"]]
Out[]=
In[]:=
UndirectedGraph[HypergraphToGraph[WolframModel[{{1,2,3}}{{1,4,6},{2,5,4},{3,6,5}},{{0,0,0}},8,"FinalState"]]];
In[]:=
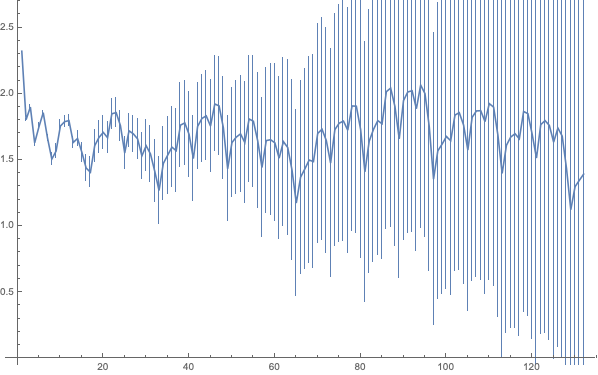
Dims[RandVols[%,200]]
Out[]=
In[]:=
UndirectedGraph[HypergraphToGraph[WolframModel[{{1,2,3}}{{1,4,6},{2,5,4},{3,6,5}},{{0,0,0}},9,"FinalState"]]];
In[]:=
Dims[RandVols[%,500]]
Out[]=
In[]:=
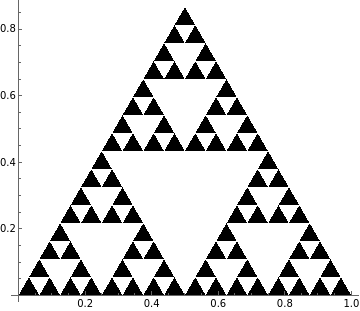
SierpinskiMesh[4]
Out[]=
In[]:=
Graphics[%250,AxesTrue]
Out[]=
In[]:=
Region[TransformedRegion[SierpinskiMesh[5],{Indexed[#,1]^2,Indexed[#,1]+Indexed[#,2]}&]]
Out[]=
Cf. limit sets of Kleinian groups.....
Model Spaces
Model Spaces
Integer dimensional lattice:
Projection function (cf. space-filling curve)
Selector of which points are allowed (e.g. BitXor on digits, or Cantor set)
Limiting to continuum when allow infinite numbers of digits, but e.g. Cantor set
Ultimately, points are labeled by their provenance in the graph rewriting system. But how does one get a good family of model spaces?
Given n digit sequences, find some consistent set in these digit sequences.
Cayley Graphs
Cayley Graphs
Add generators, then find canonical element applying all possible replacements