Universal multiway system (UMS)
Universal multiway system (UMS)
I (dh) attempt to construct a universal multiway system. My idea is: the rules and alphabet of the UMS are fixed; you feed in a chosen multiway system (MWS) init string and rules all as a single init string for the UMS. The UMS evolves this string, keeping the rules in there. A subset of resulting strings of the UMS are the strings of the MWS.
Initial format is: -----PTE--- R --- E ---R---E---R---E ... E---R---E
where the first ---- is A's and B's, and each ---R--- is something like ABA->BB (the R is the arrow; the E separates two rules). The lhs of each rule is reversed.
How it works:
1) T moves to the right. At the beginning of each rule (TE) it has the opportunity to turn into an X. X keeps moving to the right, making left-moving copies (lower case) of the letters in the rule, finally disappearing when it reaches the end of the rule.
2) Meanwhile P moves to the left. At any point, it has the opportunity to turn into a Q, which stays in place until the left-moving rule arrives. When it does, the lhs of the rule (which is in reverse order) attempts to cancel in pairs with the stuff to the left of the Q. If it fails, this branch of the UMS dies out. If it succeeds, we have Qr. Then the rhs of the rule is passed through the Qr and turned into capital letters. Then the Qr turns into a v, moves to the right, and when it encounters the rules (at the first E) turns into PTE and the process begins again.
<<"MultiwaySystems\Multiway.m"
UMS={"AP""PA","BP""PB","P""Q","TE""ET","TE""EX","TA""AT","TB""BT","TR""RT","XA""aAX","XB""bBX","XR""rRX","XE""eE","Aa""aA","Ba""aB","Ra""aR","Ea""aE","Ab""bA","Bb""bB","Rb""bR","Eb""bE","Ar""rA","Br""rB","Rr""rR","Er""rE","Ae""eA","Be""eB","Re""eR","Ee""eE","AQa""Q","BQb""Q","Qra""AQr","Qrb""BQr","Qre""v","vA""Av","vB""Bv","vE""PTE"};
Length[UMS]
36
Length@Union[Flatten[Apply[List,Map[Characters,UMS,{2}],{1}]]]
13
MWToUMS[rule_List,init_List]:=With[{r=StringJoin["PTE",{StringReverse[#〚1〛],"R",#〚2〛,"E"}&/@rule]},StringJoin[#,r]&/@init]
UMSFilter[hist_]:=StringTake[#,StringPosition[#,"P"]〚1,1〛-1]&/@Select[Flatten[hist],StringMatchQ[#,"*PT*"]&]
XMWUEvolveList[UMS,MWToUMS[{"A""AB","B""A"},{"A"}],1]
{{APTEARABEBRAE},{PATEARABEBRAE,AQTEARABEBRAE,APETARABEBRAE,APEXARABEBRAE}}
XMWUEvolveList[UMS,{"APETARABEBRAE"},46]
The above was an example of an attempted substitution that fails.
UMSFilter[XMWUEvolveList[UMS,MWToUMS[{"A""AB","B""A"},{"A"}],100]]
{A,AB,ABB,AA,AAB}
Looks good.
Graphics
Graphics
<<"MultiwaySystems/Multiway.m"
MWEvolveListT[{"A""A","A""AA"},{"A"},5]
{{{A,A}},{{A,A},{A,AA}},{{A,A},{A,AA},{AA,AA},{AA,AAA}},{{A,A},{A,AA},{AA,AA},{AA,AAA},{AAA,AAA},{AAA,AAAA}},{{A,A},{A,AA},{AA,AA},{AA,AAA},{AAA,AAA},{AAA,AAAA},{AAAA,AAAA},{AAAA,AAAAA}},{{A,A},{A,AA},{AA,AA},{AA,AAA},{AAA,AAA},{AAA,AAAA},{AAAA,AAAA},{AAAA,AAAAA},{AAAAA,AAAAA},{AAAAA,AAAAAA}}}
Show@MWGraphic[MWEvolveListT[{"A""AB","B""A"},{"A"},10],30];
Clear[MWGraphic]
MWGraphic[hist_,rightcutoff_:∞]:=Module{hh,rp,arrows,t1,t2,ellipses,hhc,rpc,arrowsc},hh=Sort[#,MWStringSortQ]&/@Union/@Map[Last,hist,{2}];rp=MapIndexed(#2〚2〛-1)1.2+StringLength[hh〚#2〚1〛,i〛],-4.4(#2〚1〛-1)&,hh,{2};rpc=Cases[#,{{x_,y_},{w_,z_}}/;x+StringLength[hh〚w,z〛]+If[z<Length[hh〚w〛],2.2,0]≤rightcutoff{x,y}]&/@MapIndexed[List,rp,{2}];hhc=MapIndexed[Take[#,Length[Extract[rpc,#2]]]&,hh];ellipses=Flatten[MapIndexed[If[Length[hh〚#2〚1〛〛]Length[#],{},{rp〚#2〚1〛,Length[#]+1〛}]&,hhc],1];arrows=FlattenTablet1=Position[hh〚y-1〛,hist〚y,x,1〛,1,1]1,1;t2=Position[hh〚y〛,hist〚y,x,2〛,1,1]1,1;rpy-1,t1+StringLength[hh〚y-1,t1〛],-.3,rpy,t2+StringLength[hh〚y,t2〛],1.3,{y,2,Length[hist]},{x,1,Length[hist〚y〛]},1;arrowsc=Cases[arrows,{{w_,x_},{y_,z_}}/;w≤rightcutoff||y≤rightcutoffIf[w>rightcutoff,Arrow[{{rightcutoff,z+(x-z)(rightcutoff-y)/(w-y)},{y,z}},.5,ArrowStyleAbsoluteThickness[.25]],If[y>rightcutoff,Line[{{w,x},{rightcutoff,x+(z-x)(rightcutoff-w)/(y-w)}}],Arrow[{{w,x},{y,z}},.5,ArrowStyleAbsoluteThickness[.25]]]]];Graphics[{MapThread[rowblock2,{Flatten[hhc,1],Flatten[rpc,1]}],{AbsolutePointSize[.5],GrayLevel[0],Point[#+{0,.5}],Point[#+{.5,.5}],Point[#+{1,.5}]}&/@ellipses,arrowsc},AspectRatioAutomatic]
#2〚2〛-1
∑
i=1
1
2
1
2
General::spell1:Possible spelling error: new symbol name "arrowsc is similar to existing symbol arrows.
UMSIcon["A"][off_]:={Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["B"][off_]:={GrayLevel[0],Rectangle[off+{0,0},off+{1,1}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["R"][off_]:={GrayLevel[.5],Rectangle[off+{0,0},off+{1,1}],GrayLevel[1],Polygon[off+#&/@{{.25,.4},{.25,.6},{.55,.6},{.55,.8},{.75,.5},{.55,.2},{.55,.4}}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["a"][off_]:={GrayLevel[1],Rectangle[off+{0,0},off+{1,1}],GrayLevel[0],Line[off+#&/@{{.35,.5},{.6,.7},{.6,.3},{.35,.5}}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["b"][off_]:={GrayLevel[0],Rectangle[off+{0,0},off+{1,1}],GrayLevel[1],Line[off+#&/@{{.35,.5},{.6,.7},{.6,.3},{.35,.5}}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["r"][off_]:={GrayLevel[.5],Rectangle[off+{0,0},off+{1,1}],GrayLevel[1],AbsoluteThickness[.25],Line[off+#&/@{{.25,.4},{.25,.6},{.55,.6},{.55,.8},{.75,.5},{.55,.2},{.55,.4},{.25,.4}}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["e"][off_]:={GrayLevel[.5],Rectangle[off+{0,0},off+{1,1}],GrayLevel[1],AbsoluteThickness[.25],Line[off+#&/@{{.4,.1},{.4,.9},{.6,.9},{.6,.1},{.4,.1}}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["Q"][off_]:={GrayLevel[.5],Rectangle[off+{0,0},off+{1,1}],GrayLevel[0],Rectangle[off+{.4,.1},off+{.6,.9}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["T"][off_]:={GrayLevel[.5],Rectangle[off+{0,0},off+{1,1}],GrayLevel[1],Polygon[off+#&/@{{.65,.5},{.4,.7},{.4,.3},{.65,.5}}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["X"][off_]:={GrayLevel[.5],Rectangle[off+{0,0},off+{1,1}],GrayLevel[1],Line[off+#&/@{{.65,.5},{.4,.7},{.4,.3},{.65,.5}}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["P"][off_]:={GrayLevel[.5],Rectangle[off+{0,0},off+{1,1}],GrayLevel[0],Polygon[off+#&/@{{.35,.5},{.6,.7},{.6,.3},{.35,.5}}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
UMSIcon["v"][off_]:={GrayLevel[.5],Rectangle[off+{0,0},off+{1,1}],GrayLevel[0],Polygon[off+#&/@{{.65,.5},{.4,.7},{.4,.3},{.65,.5}}],Sequence@@GrayStyle,Line[off+#&/@{{0,0},{0,1},{1,1},{1,0},{0,0}}]}
Show@Graphics[MapIndexed[UMSIcon[#][{First[#2],0}]&,{"A","B","R","E","a","b","r","e","P","Q","T","X","v"}],AspectRatioAutomatic];
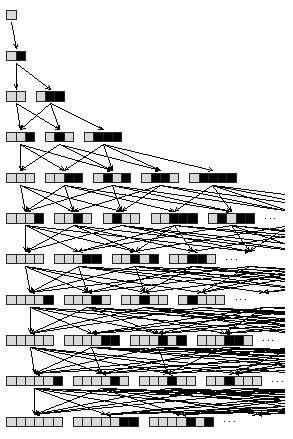
UMSGraphic[hist_,rightcutoff_:∞]:=Module{hh,rp,arrows,t1,t2,ellipses,hhc,rpc,arrowsc},hh=Sort[#,MWStringSortQ]&/@Union/@Map[Last,hist,{2}];rp=MapIndexed(#2〚2〛-1)1.2+StringLength[hh〚#2〚1〛,i〛],-4.4(#2〚1〛-1)&,hh,{2};rpc=Cases[#,{{x_,y_},{w_,z_}}/;x+StringLength[hh〚w,z〛]+If[z<Length[hh〚w〛],2.2,0]≤rightcutoff{x,y}]&/@MapIndexed[List,rp,{2}];hhc=MapIndexed[Take[#,Length[Extract[rpc,#2]]]&,hh];ellipses=Flatten[MapIndexed[If[Length[hh〚#2〚1〛〛]Length[#],{},{rp〚#2〚1〛,Length[#]+1〛}]&,hhc],1];arrows=FlattenTablet1=Position[hh〚y-1〛,hist〚y,x,1〛,1,1]1,1;t2=Position[hh〚y〛,hist〚y,x,2〛,1,1]1,1;rpy-1,t1+StringLength[hh〚y-1,t1〛],-.3,rpy,t2+StringLength[hh〚y,t2〛],1.3,{y,2,Length[hist]},{x,1,Length[hist〚y〛]},1;arrowsc=Cases[arrows,{{w_,x_},{y_,z_}}/;w≤rightcutoff||y≤rightcutoffIf[w>rightcutoff,Arrow[{{rightcutoff,z+(x-z)(rightcutoff-y)/(w-y)},{y,z}},.5,ArrowStyleAbsoluteThickness[.25]],If[y>rightcutoff,Line[{{w,x},{rightcutoff,x+(z-x)(rightcutoff-w)/(y-w)}}],Arrow[{{w,x},{y,z}},.5,ArrowStyleAbsoluteThickness[.25]]]]];Graphics[{MapThread[MapIndexed[Function[{z,w},UMSIcon[z][#2+{First[w]-1,0}]],Characters[#]]&,{Flatten[hhc,1],Flatten[rpc,1]}],{AbsolutePointSize[.5],GrayLevel[0],Point[#+{0,.5}],Point[#+{.5,.5}],Point[#+{1,.5}]}&/@ellipses,arrowsc},AspectRatioAutomatic]
#2〚2〛-1
∑
i=1
1
2
1
2