FindEmbeddingX[g_,excl_,d_:2,wf_:(1&),s_:1234,opts___]:=Module[{i,n=Length[g]},m=DistanceMatrix[g,excl];c=Apply[Plus,Flatten[ReplacePart[Map[wf,m,{2}](TrialMatrix[n,d]-m^2),0,Flatten[Outer[List,excl,excl],1]]]^2];vars=Flatten[Table[x[i,j],{i,2,n},{j,d}]];con=Table[x[1,i]->0,{i,d}];SeedRandom[s];ans=FindMinimum[Evaluate[c/.con],##,opts]&@@({#,Random[]}&/@vars);ans2=Prepend[Partition[vars/.Last[ans],d],Table[0,{d}]];ans3=Map[ans2[[#]]&,NodesToEdges[g],{-1}];{ans2,If[d==2,Graphics,Graphics3D][Line/@ans3,AspectRatio->Automatic]}]
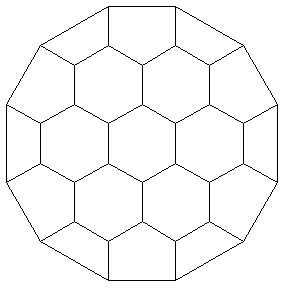
Line/@Lines2D[2];
RimNodes2D[%93]
{1,2,3,6,11,16,21,26,31,34,35,36}
Show[AddRim2D[%93]];
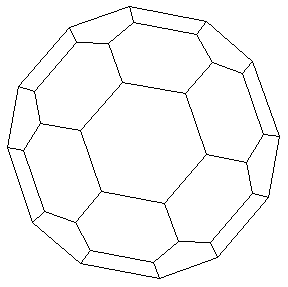
The following is an earlier result, not leaving the rim nodes out of the DistanceMatrix computation:
FindEmbeddingX[ReverseEngineer[%99],%98];
Show[Last[%]];
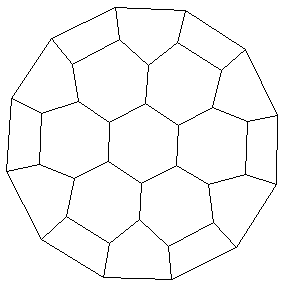
This is the correct result:
FindEmbeddingX[ReverseEngineer[%99],%98];
Show[Last[%]];
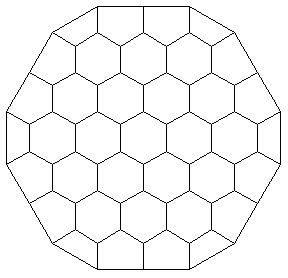
Line/@Lines2D[3];
RimNodes2D[%]
{1,2,3,6,7,12,19,26,33,40,47,54,61,66,67,70,71,72}
Show[AddRim2D[%%]];
FindEmbeddingX[ReverseEngineer[%224],%225];
Show[Last[%]];