NeighborsPicture[g_,init_]:=Module[{connectedNodes,selfLoopNodeQ,toLines,toCircles,toSelfLoopCircles,nodePosition,g1,allNodes,graphicsBag,activeNodes,xCoord,usedNodes,nextNodes,nextNodes1},selfLoopNodeQ[n_]:=MemberQ[g,n->_List?(Count[#,n]===2&)];connectedNodes[l_]:=First/@Cases[ap=Apply[{{##},MemberQ[#1/.g,#2]&&MemberQ[#2/.g,#1]}&,so=(Sort/@Flatten[Table[{l[[i]],l[[j]]},{i,Length[l]},{j,i+1,Length[l]}],1]),{1}],{_,True}];toLines[{startNode_,endNodes_}]:=Line[{nodePosition[startNode],nodePosition[#]}]&/@endNodes;toSelfLoopCircles[node_]:=With[{mp=nodePosition[node]},{Circle[mp+{0,1/8},{1/4,1/8},{-Pi/2,Pi/2}],Circle[mp+{0,0},{1/4,1/4},{Pi/2,3Pi/2}],Circle[mp+{0,-1/8},{1/4,1/8},{-Pi/2,Pi/2}]}];toCircles[{node1_,node2_}]:=With[{mp1=nodePosition[node1],mp2=nodePosition[node2]},Circle[(mp1+mp2)/2,{1/2,Abs[mp1[[2]]-mp2[[2]]]/2},{-Pi/2,Pi/2}]];g1=Flatten/@Apply[List,g,{1}];allNodes=First/@g;graphicsBag={};activeNodes={allNodes[[init[[1]]]]};nodePosition[init[[1]]]={0,0};xCoord=1;usedNodes=activeNodes;If[selfLoopNodeQ[init[[1]]],AppendTo[graphicsBag,toSelfLoopCircles[init[[1]]]]];While[Union[(nextNodes=DeleteCases[activeNodes/.g,Alternatives@@usedNodes,{2}])]=!={{}},(*useeverynewnodeonlyonce*)nextNodes1=Delete[nextNodes,Last/@Select[Position[nextNodes,#]&/@Sort[Flatten[nextNodes]],{_,_}]];(*positionsofthenewnodes*)Apply[(nodePosition[#1]={xCoord,#2})&,First@Fold[{Append[#[[1]],Take[#[[2]],#2]],Drop[#[[2]],#2]}&,{{},MapIndexed[{#,#2[[1]]-1}&,Flatten[nextNodes1]]},Length/@nextNodes1],{-2}];(*thenewnodeconnections*)AppendTo[graphicsBag,{toLines/@Transpose[{activeNodes,nextNodes1}],toCircles/@connectedNodes[Flatten[nextNodes1]],toSelfLoopCircles/@Select[Flatten[nextNodes1],selfLoopNodeQ]}];usedNodes=Join[usedNodes,Flatten[nextNodes1]];activeNodes=Flatten[nextNodes1];xCoord=xCoord+1];Show[Graphics[{graphicsBag,Text[FontForm[ToString[#],{"Courier-Bold",14}],nodePosition[#]-{1/8,0}]&/@allNodes}]]];
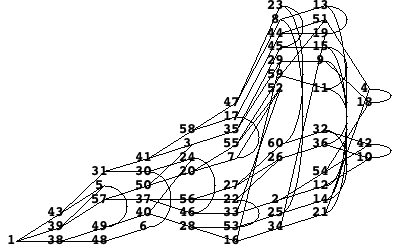
NeighborsPicture[RandomNetwork[60],{1}]
⁃Graphics⁃
NeighborsPicture[RandomNetwork[100],{1}]
⁃Graphics⁃