Ada Lovelace, Bernoulli and the Gauss Schoolboy Problem
Ada Lovelace, Bernoulli and the Gauss Schoolboy Problem
Introduction to Ada Lovelace
Introduction to Ada Lovelace
Ada Lovelace was an English mathematician and writer. She is chiefly known for her work on Charles Babbage’s early mechanical general-purpose computer, the Analytical Engine. She is considered the first female computer programmer due to her work on Bernoulli numbers. Read more about Ada Lovelace in Stephen Wolfram’s blog post, Untangling the Tale of Ada Lovelace.
The Gauss Schoolboy Problem
The Gauss Schoolboy Problem
There’s a well-known story about the famous German mathematician Carl Friedrich Gauss. As a young schoolboy, he was tasked with adding the first 100 integers, i.e. what is 1 + 2 + 3 + 4 + ... + 98 + 99 + 100? (The answer is 5,050.) Gauss reportedly produced the correct answer within seconds.How did he do this?The trick is to pair the numbers 1 + 100, 2 + 99, 3 + 98..., 50 + 51 to get 50 x 51 = 5,050.Can we easily calculate the sum of the squares of the numbers 1 to 100 today? Yes! Using computers and programming, there are several ways to do so.
Introduction to the Wolfram Language
Introduction to the Wolfram Language
Using the built-in functions available in the Wolfram Language, it is elementary to calculate this quantity. In fact, there is more than one way to do it using Wolfram Language technology. Before you can explore that, this section will provide an introduction to the Wolfram Language.
Let’s try to do something simple first.Click the line below and press Shift + Enter ( + ).
↓
In[]:=
1+2+3
You should have gotten the output 6.
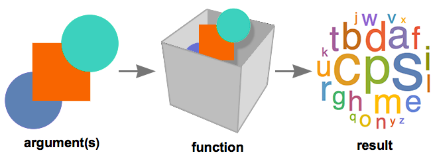
Functions
Functions
All calculations in Mathematica are done by calling functions.You can think of each function as a box. Into each box we put arguments, and then the box spits out a result.
Evaluate the Following Examples
Evaluate the Following Examples
(Click next to the inputs below, hold down and press .)
↓
In[]:=
Divide[65,5]
In[]:=
Expand[(a+b)^2]
Introduction to Bernoulli Numbers
Introduction to Bernoulli Numbers
Let’s try a simpler version of the Gauss schoolboy problem: calculating the sum of the first two integers, i.e. 1 + 2, and then increasing the sum steadily.
We see that here:1 + 2 = 31 + 2 + 3 = 61 + 2 + 3 + 4 = 101 + 2 + 3 + 4 + 5 = 15The sequence of numbers generated in this manner are 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406...There’s a formula that can calculate this sum.You may know the sum of the first n integers, i.e. 1 + 2 + 3 + ... + (n – 1) + n = n(n + 1)/2.How would we generalize this process of adding integers together? The Wolfram Language built-in function Sum can help.
Sum[k,{k,n}]
1
2
Sum[i, {i,n}] evaluates .
n
∑
i=1
i
Expanding this result, we see the following:
Expand[(1/2)n(1+n)]
n
2
2
n
2
Note the (1/2).
What about Squares?
What about Squares?
Expressing the sum of squares in the same fashion as we did earlier, we get the following equations: + = 1 + 4 = 5 + + = 1 + 4 + 9 = 14 + + + = 1 + 4 + 9 + 16 = 30 + + + + = 1 + 4 + 9 + 16 + 25 = 55
2
1
2
2
2
1
2
2
2
3
2
1
2
2
2
3
2
4
2
1
2
2
2
3
2
4
2
5
Using Sum to evaluate the sum of squares, we get:
Sum[i^2,{i,n}]
1
6
Expanding this sum, we see that:
Expand[(1/6)(1+n)(n+2n^2)]
n
6
2
n
2
3
n
3
Note the (1/6).
And Cubes
And Cubes
By now, you get the idea of what we are doing here.
What about the sum of cubes? Is there a general formula that expresses this relation?
What about the sum of cubes? Is there a general formula that expresses this relation?
Sum[i^3,{i,0}]
Expanding this result gives:
Note there is no term with n.
Call These Leading Terms the Bernoulli Numbers
Call These Leading Terms the Bernoulli Numbers
Solve the equation for the sum of fourth powers:
With the following Wolfram Language code, we can visualize the first 100 Bernoulli numbers by color: Positive Bernoulli numbers are indicated by Blue, negative Bernoulli numbers by Red, and the slots where the Bernoulli number is 0 is indicated by Gray.
Ada’s original letter, mentioning the Bernoulli numbers
Advances in Programming Today
Advances in Programming Today
Further Reading
Further Reading
Want to check out the Wolfram Language and see what you can do with it? Check out these free resources:
Ada Lovelace, Bernoulli and the Gauss Schoolboy Problem
Ada Lovelace, Bernoulli and the Gauss Schoolboy Problem