In[]:=
S[q_]:=Simplify[Plus@@(Cot[Pi#/q]^2&/@Select[Range[q-1],GCD[#,q]==1&])];
In[]:=
Phi2[q_]:=q^2Times@@((1-1/#[[1]]^2)&/@FactorInteger[q]);
In[]:=
SBM[q_?IntegerQ]:=1/3Phi2[q]-EulerPhi[q];
In[]:=
SBM[22071945]
Out[]=
135744984254976
In[]:=
FullSimplify[S[100]]//Timing
Out[]=
{63.2377,2360}
In[]:=
SBM[100]//Timing
Out[]=
{0.00014,2360}
In[]:=
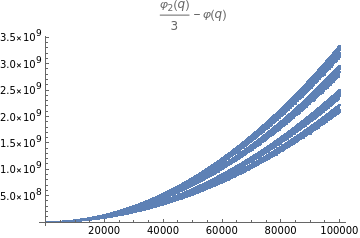
SMdata={#,SBM[#]}&/@Range[10,100000];
In[]:=
ListPlot[SMdata,PlotLabel->Subscript[φ,2][q]/3-φ[q]]
Out[]=
In[]:=
SBM[9]
Out[]=
18
In[]:=
9^2(1-1/9)/3-9(1-1/3)
Out[]=
18
In[]:=
Table[{q,SBM[q]},{q,2,10}]
Out[]=
{2,0},3,,{4,2},{5,4},{6,6},{7,10},{8,12},{9,18},{10,20}
2
3
6^2(1-1/9)(1-1/4)/3=(3-1)(3+1)(2-1)(2+1)/3
Out[]=
8
In[]:=
Table[Phi2[q]/3,{q,3,20}]
Out[]=
,4,8,8,16,16,24,24,40,32,56,48,64,64,96,72,120,96
8
3
In[]:=
SBM[2^64+1]
Out[]=
113427455638803936117726648213506949120
In[]:=
SBM[2^64]
Out[]=
85070591730234615856620279821087277056
In[]:=
SBM[2^128+1]
Out[]=
38597363079105398474523661669562625103150274109036501299425668761748925317120
In[]:=
SBM[Prime[200000]]
Out[]=
2521122091602
In[]:=
SBM[Prime[200000]+1]
Out[]=
1580590852608