2
cot
β
2
4
π
∫
-π
dω
2π
ωqr
e
N-2
cos
2
sin
(*expandthebinomialinCos[ω]^Landintegratetermbytermanalyticallypickthes-term(E^(Iωs)E^(-Iω(L-s)))Binomial[L,s]*)
In[]:=
HH=Expand[E^(Iωq)TrigToExp[Sin[ω]^2]/.(+)^L_:>Binomial[L,s]E^(Iωs-Iω(L-s))]
-2+N
Cos[ω]
-ω
ω
Out[]=
1-N
2
qω-(-2+N-s)ω+sω
-N
2
-2ω+qω-(-2+N-s)ω+sω
-N
2
2ω+qω-(-2+N-s)ω+sω
In[]:=
ClearAll[subInt];
In[]:=
subInt[s_]={E^(X_)F_:>(F/.Solve[D[X,ω]==0,s][[1]])}
Out[]=
F_(F/.Solve[X0,s]〚1〛)
X_
∂
ω
(*thissubstitutionisequivalenttointegrationoverω--selectionoftheconstantterminbinomialexpansion*)
In[]:=
JJ[q_]=FullSimplify[HH/.subInt[s]]
Out[]=
-Binomial-2+N,(-4+N-q)-2Binomial-2+N,(-2+N-q)+Binomial-2+N,
-N
2
1
2
1
2
N-q
2
In[]:=
1/4Cot[Pip/q]^2Binomial-2+N,(-2+N-q)FullSimplifyJJ[q]Binomial-2+N,(-2+N-q)/.q->qr
1
2
1
2
Out[]=
-N
2
2
q
2
r
1
2
2
Cot
pπ
q
2
N
2
q
2
r
(N-)
2
q
2
r
2
cot
β
2
N
2
2
N
2
q
2
r
N-2 |
1 2 |
In[]:=
-N
2
2
q
2
r
1
2
2
Cot
pπ
q
2
N
2
q
2
r
Out[]=
-5-N
2
2
q
2
r
2
Cot
pπ
q
Gamma(2+N-qr)Gamma(2+N+qr)
1
2
1
2
-N-5
2
2
cot
πp
q
2
q
2
r
Γ(N-qr+2)Γ(N+qr+2)
1
2
1
2
In[]:=
asymp=NormalSeries(N-N)Gamma[1+N],{N,Infinity,2}
-5-N
2
2
z
Gamma(2+N-zSqrt[N])Gamma(2+N+zSqrt[N])
1
2
1
2
Out[]=
-)+(-1+)(3-6+)-(-45+705-1230+678-113+5)
-
2
z
2
N
(-1+2
z
16
2π
-
2
z
2
2
z
2
z
4
z
192
N
2π
-
2
z
2
2
z
4
z
6
z
8
z
10
z
23040
3/2
N
2π
In[]:=
Integrate[asymp,{z,-Infinity,Infinity}]
Out[]=
0
In[]:=
N
64
π
Out[]=
N
3/2
π
1728Zeta[3]
In[]:=
IIodd[M_?OddQ,q_?OddQ]:=2Sum[(M-s^2)Binomial[M,(M+s)/2],{s,q,M,2q}]//Quiet;
-5-M
2
In[]:=
testprime=With[{MM=101},ParallelTable[{q,IIodd[MM,q]},{q,3,MM-1,2}]];
In[]:=
Max[N[testprime]]
Out[]=
99.
In[]:=
Min[N[testprime]]
Out[]=
-0.224218
In[]:=
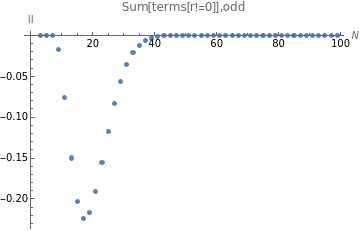
ListPlot[testprime,PlotLabel->"Sum[terms[r!=0]],odd",AxesLabel->{N,II}]
Out[]=
In[]:=
IIeven[M_,q_?EvenQ]:=2Sum[(M-s^2)Binomial[M,(M+s)/2],{s,q,M,q}]//Quiet;
-5-M
2
In[]:=
IIeven[M_,q_?OddQ]:=2Sum[(M-s^2)Binomial[M,(M+s)/2],{s,2q,M,2q}]//Quiet;
-5-M
2
In[]:=
NormalSeries(N-qr^2)Gamma[1+N],{N,Infinity,2}
-5-N
2
Gamma(2+N-qr)Gamma(2+N+qr)
1
2
1
2
Out[]=
N
16
2π
1+6
2
qr
64
N
2π
1+28+20
2
qr
4
qr
512
3/2
N
2π
In[]:=
test1=ParallelTable[{M,II[M,M/2]},{M,100000,150000}];
In[]:=
ListPlot[test1]
Out[]=
In[]:=
lmm=LinearModelFit[test1,{x,x^2},x]
In[]:=
ShowFitLogModel[data_,model_,Ylabel_,title_]:=Show[ListPlot[data,PlotStyle->{Red,PointSize[0.01]},PlotLegends->{"data"}],Plot[Exp[model[Log[x]]],{x,data[[1,1]],data[[-1,1]]},PlotStyle->{Green,Thick},PlotLegends->{N[Exp[model[Log[N]]],7]},PlotRange->All],PlotLabel->title,AxesLabel->{"N",Ylabel}];
In[]:=
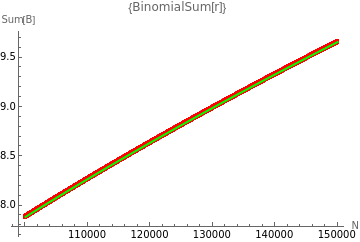
ShowFitLogModel[test1,loglmm,"Sum[B]",{"BinomialSum[r]"}]
Out[]=
In[]:=
lognlmm=NonlinearModelFit[Log[test1],{a+1/2x},{a},x]
Out[]=
FittedModel
In[]:=
Normal[lognlmm]
Out[]=
-3.6915292827711146537+
x
2
In[]:=
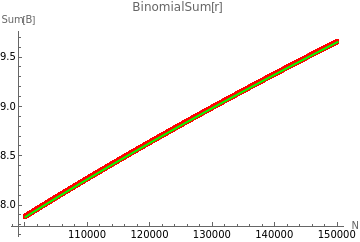
ShowFitLogModel[test1,lognlmm,"Sum[B]","BinomialSum[r]"]
Out[]=