Finding the Sniper that Shot Charlie Kirk
Question: Where was the sniper that shot Charlie Kirk?
The crack-thump analysis is a method used to estimate the distance to a sniper’s position by leveraging the difference in arrival times of two distinct sounds: the “crack” of the bullet’s sonic boom and the “thump” of the rifle’s muzzle blast.
The crack-thump analysis is a method used to estimate the distance to a sniper’s position by leveraging the difference in arrival times of two distinct sounds: the “crack” of the bullet’s sonic boom and the “thump” of the rifle’s muzzle blast.
The Physics Behind the Sounds of Gunfire
A rifle fires a bullet that travels faster than the speed of sound. As this supersonic projectile moves through the air, it creates a shockwave, which is heard by an observer as a sharp, distinct “crack.” This is the first sound that reaches a target.
The “thump” is the sound of the actual gunshot, the muzzle blast created by the expanding gases from the rifle’s barrel. This sound travels at the speed of sound, which is significantly slower than the supersonic bullet.
Because the “crack” (the bullet’s sonic boom) travels at the speed of the bullet and the “thump” (the muzzle blast) travels at the speed of sound, there is a time delay between when each is heard. This delay increases with the distance between the sniper and the observer. By measuring this time interval, one can estimate the distance to the sniper.
The “thump” is the sound of the actual gunshot, the muzzle blast created by the expanding gases from the rifle’s barrel. This sound travels at the speed of sound, which is significantly slower than the supersonic bullet.
Because the “crack” (the bullet’s sonic boom) travels at the speed of the bullet and the “thump” (the muzzle blast) travels at the speed of sound, there is a time delay between when each is heard. This delay increases with the distance between the sniper and the observer. By measuring this time interval, one can estimate the distance to the sniper.
A Note on Historical Use
While the informal “crack-thump” method has likely been understood by soldiers for as long as supersonic firearms have existed, a more formalized and technologically advanced version of this principle, known as sound ranging, was notably employed during World War I. The British Army developed a sophisticated system that used multiple microphones to detect the sound of enemy artillery. By analyzing the different arrival times of the gunshot’s sound at these various points, they could triangulate the position of the enemy guns with remarkable accuracy, sometimes to within 10 meters. This early application of acoustic science on the battlefield laid the groundwork for modern sniper detection systems.
While the informal “crack-thump” method has likely been understood by soldiers for as long as supersonic firearms have existed, a more formalized and technologically advanced version of this principle, known as sound ranging, was notably employed during World War I. The British Army developed a sophisticated system that used multiple microphones to detect the sound of enemy artillery. By analyzing the different arrival times of the gunshot’s sound at these various points, they could triangulate the position of the enemy guns with remarkable accuracy, sometimes to within 10 meters. This early application of acoustic science on the battlefield laid the groundwork for modern sniper detection systems.
Equations for Crack-Thump Analysis
Equations for Crack-Thump Analysis
Ranging Enemy Fire by Calculating the Distance from a Sniper using Audio on the Target ≡ velocity of sound ≡ velocity of bulletdistance ≡ distance between gun and microphone which should be be near the target ≡ time for sound to travel over the distance ≡ time for bullet to travel over the distance (1) (2) = (3) = (4)Subtracting equation (4) from (3): - - (5) = - (6)distance ( - ) (7)distance (8)
velocity
1
velocity
2
time
1
time
2
distance
velocity
1
time
1
distance
velocity
2
time
2
distance
velocity
1
time
1
distance
velocity
2
time
2
distance
velocity
1
distance
velocity
2
=
time
1
time
2
Δtime
time
1
time
2
1
velocity
1
1
velocity
2
=Δtime
=-
Δtime
1
velocity
1
1
velocity
2
How Far Away Was the Sniper that Shot Charlie Kirk?
How Far Away Was the Sniper that Shot Charlie Kirk?
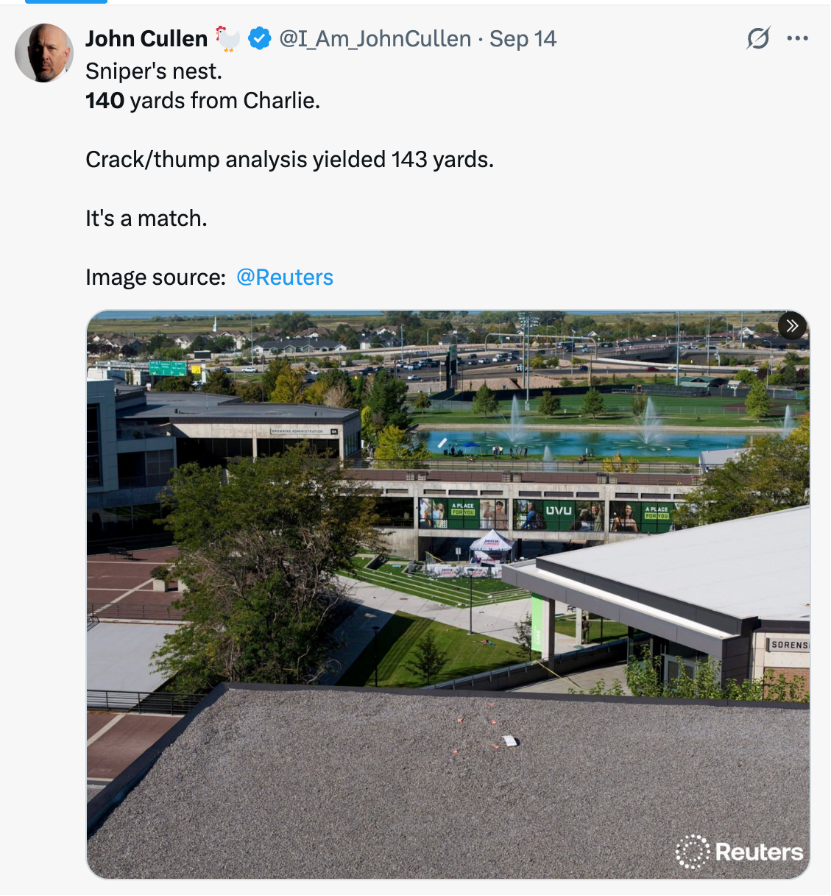
Let’s apply the equations to the suspicious shooting of Charlie Kirk. From John Cullen, Δtime ≡ 0.23 seconds.At 80°F, 30% humidity and 5000 feet elevation, the AI estimated speed of sound as ≡ 1136 feet per second.The muzzle velocity of a .30-06 Springfield cartridge from M2 Ball ammunition fired from a speculated Remington 700 rifle: ≡ 3000 feet per second
velocity
1
velocity
2
In[]:=
0.23 / (1/1136 - 1/3000)
Out[]=
420.515
Convert from feet to yards
In[]:=
420/3
140
This agrees with John’s estimated distance of Sniper’s Nest based measurement of Utah Valley University campus. Also is close to his independent crack/thump analysis.