Wolfram Cloud Document

In[]:=

Clear["Global`*"];ω=2000;c1[ζ_]:=-ζω+ω

2

ζ

-1

;c2[ζ_]:=-ζω-ω

2

ζ

-1

;H[ζ_]:=

2

ω

(s-c1[ζ])(s-c2[ζ])

;

StepR[t_,ζ_]:=

2

ω

(c1[ζ]-c2[ζ])

*

c1[ζ]t



-1

c1[ζ]

-

c2[ζ]t



-1

c2[ζ]

(*UnitImpulseIntegratedbyhandUnitstepResponse*)

H1=

2

ω

2

(s+ω)

(*Transferfunctionwhenζ=1*)(*RelevantTimeDomainFunctiont*

-ωt



*u(t)StepR1meanstheIntegralofitasbelow*)

In[]:=

StepR1[t_]:=

2

ω

t

∫

0

τ*Exp[-ωτ]*UnitStep[τ]τ

In[]:=

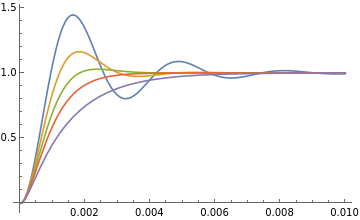
Plot[{StepR[t,0.25],StepR[t,0.5],StepR[t,0.75],StepR1[t],StepR[t,1.5]},{t,0,0.010},PlotRangeAll,PlotLegends"Expressions"]

Out[]=

	StepR(t,0.25)
	StepR(t,0.5)
	StepR(t,0.75)
	StepR1(t)
	StepR(t,1.5)

In[]:=

Manipulate[Control`PoleZeroPlot[{H[ζ]},PlotLabelStringForm["Pole Zero Plot for ζ = `1`",ζ],PlotLegendsStringForm["ζ = `1` ",ζ],PoleZeroMarkersStyle["x",Large,BackgroundCyan],AxesLabel{"Re","Im"}],{{ζ,0.5},0,1}]

Out[]=

ζ

ζ = 0.5