How to evaluate
1
∫
0
ln(x)(1+ln(x)+ln(1−x))
2
x
+1
dx

In[]:=
ClearAll["Global`*"]
In[]:=
Hyperlink["evaluate int","https://math.stackexchange.com/questions/4832089/how-to-evaluate-int-0-1-frac-ln-x1-lnx-ln1-xx21dx"]
Out[]=
evaluate int
◼
  • Integrand
    • In[]:=
    f[x_]:=
    Log[x](1+Log[x]+Log[1-x])
    2
    x
    +1
    In[]:=
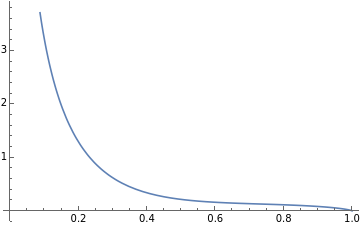
    Plot[f[x],{x,0,1}]
    Out[]=
    In[]:=
    F[x_]=∫f[x]x
    Out[]=
    -
    1
    2
    -Log[1-x]Log[x]+Log[1+x]Log[x]-Log[1-x]
    2
    Log[x]
    +Log[1+x]
    2
    Log[x]
    -
    1
    2
    Log[-x](-2Log[1-x]+Log[-x])Log[1+x]-Log
    1
    2
    +
    
    2
    (-+x)+Log[-x]Log
    (1+)x
    -1+x
    Log[1+x]-Log
    1
    2
    +
    
    2
    (-+x)+Log[1-x]Log[x]Log
    1
    2
    +
    
    2
    (-+x)+
    1
    2
    2
    Log
    (1+)x
    -1+x
    
    Log
    1
    1-x
    -Log
    1+x
    1-x
    +Log
    1
    2
    +
    
    2
    (-+x)+
    1
    2
    Log[x](-2Log[1-x]+Log[x])Log[1-x]-Log
    1
    2
    -
    
    2
    (+x)-Log[x]Log
    (1-)x
    -1+x
    Log[1-x]-Log
    1
    2
    -
    
    2
    (+x)-Log[1-x]Log[x]Log
    1
    2
    -
    
    2
    (+x)-
    1
    2
    2
    Log
    (1-)x
    -1+x
    
    Log
    1
    1-x
    +Log
    1
    2
    -
    
    2
    (+x)-Log
    (+x)
    -1+x
    +Log[x]-Log
    (1+)x
    -1+x
    PolyLog2,-
    1
    2
    -
    
    2
    (-1+x)-Log[x]-Log
    (1-)x
    -1+x
    PolyLog2,-
    1
    2
    +
    
    2
    (-1+x)+PolyLog[2,-x]+2Log[x]PolyLog[2,-x]+Log[1-x]+Log
    (1+)x
    -1+x
    PolyLog[2,-x]-PolyLog[2,x]-2Log[x]PolyLog[2,x]-Log[1-x]+Log
    (1-)x
    -1+x
    PolyLog[2,x]-Log
    (1-)x
    -1+x
    PolyLog2,
    x
    -1+x
    -PolyLog2,
    (1-)x
    -1+x
    +Log
    (1+)x
    -1+x
    PolyLog2,
    x
    -1+x
    -PolyLog2,
    (1+)x
    -1+x
    -PolyLog3,-
    1
    2
    -
    
    2
    (-1+x)+PolyLog3,-
    1
    2
    +
    
    2
    (-1+x)-3PolyLog[3,-x]+3PolyLog[3,x]-PolyLog3,
    (1-)x
    -1+x
    +PolyLog3,
    (1+)x
    -1+x
    
    In[]:=
    F0=
    
    x
    +
    0
    F[x]
    Out[]=
    1
    64
    
    2
    π
    4Log
    1
    2
    -
    
    2
    -Log
    1
    2
    +
    
    2
    +4π4Log[-1-]Log
    1
    2
    -
    
    2
    -Log
    1
    2
    +
    
    2
    Log[2]+6PolyLog2,
    1
    2
    -
    
    2
    -44
    2
    Log[-1-]
    Log
    1
    2
    -
    
    2
    -Log
    1
    2
    +
    
    2
    
    2
    Log[2]
    +Log[16]PolyLog2,
    1
    2
    -
    
    2
    -8Log[-1-]PolyLog2,
    1
    2
    +
    
    2
    +8PolyLog3,
    1
    2
    -
    
    2
    -8PolyLog3,
    1
    2
    +
    
    2
    
    In[]:=
    F1=
    
    x
    -
    1
    F[x]
    Out[]=
    1
    192
    18
    3
    π
    -96Catalan(2+Log[2])+12π-3
    2
    Log[1-]
    +Log-
    1
    2
    +
    
    2
    +Log[1+]Log[2]-
    2
    π
    16Log[-1-]-3Log[-1+]+16Log
    1
    2
    -
    
    2
    +16Log[1-]+3Log[1+]+Log[16]-412Log[-1-]
    2
    Log
    1
    2
    -
    
    2
    
    +4
    3
    Log
    1
    2
    -
    
    2
    
    +4
    3
    Log[1-]
    -6
    2
    Log[1-]
    Log[2]+3Log[-1+]
    2
    Log[2]
    -3Log[1+]
    2
    Log[2]
    -72PolyLog[3,-]+72PolyLog[3,]
    In[]:=
    ΔF=F1-F0//Simplify
    Out[]=
    1
    192
    18
    3
    π
    -96Catalan(2+Log[2])-
    2
    π
    16Log[-1-]-3Log[-1+]+28Log
    1
    2
    -
    
    2
    -3Log
    1
    2
    +
    
    2
    +16Log[1-]+3Log[1+]+Log[16]-12π4Log[-1-]Log
    1
    2
    -
    
    2
    +3
    2
    Log[1-]
    -Log-
    1
    2
    +
    
    2
    Log[2]-Log
    1
    2
    +
    
    2
    Log[2]-Log[1+]Log[2]+6PolyLog2,
    1
    2
    -
    
    2
    +412
    2
    Log[-1-]
    Log
    1
    2
    -
    
    2
    -4
    3
    Log
    1
    2
    -
    
    2
    
    -4
    3
    Log[1-]
    -3Log[-1+]
    2
    Log[2]
    -3Log
    1
    2
    +
    
    2
    
    2
    Log[2]
    +3Log[1+]
    2
    Log[2]
    +
    2
    Log[1-]
    Log[64]+3Log[16]PolyLog2,
    1
    2
    -
    
    2
    -12Log[-1-]
    2
    Log
    1
    2
    -
    
    2
    
    +2PolyLog2,
    1
    2
    +
    
    2
    +72PolyLog[3,-]-72PolyLog[3,]+24PolyLog3,
    1
    2
    -
    
    2
    -24PolyLog3,
    1
    2
    +
    
    2
    
    ◼
  • Result
    • In[]:=
    dF=ΔF//Re//ComplexExpand//FullSimplify
    Out[]=
    1
    128
    -128Catalan+7
    3
    π
    -4π
    2
    Log[2]
    +64PolyLog3,
    1
    2
    -
    
    2
    -PolyLog3,
    1
    2
    +
    
    2
    
    ◼
  • Numerical value of Result
    • In[]:=
    N[dF,20]
    Out[]=
    1.30259920452418087031+0.×
    -21
    10
    
    ◼
  • Verify with numerical integration
    • In[]:=
    NIntegrate[f[x],{x,0,1},WorkingPrecision->20]
    Out[]=
    1.3025992045241808709