Code
Code
Take any MultiwayGraph
In[]:=
mwg=NestGraph[x|->StringReplaceList[x,"A"->"AB"],"AA",5];
In[]:=
Graph[mwg,VertexLabelsAutomatic]
Out[]=
Get some foliations of it:
In[]:=
foliations=ResourceFunction["GraphFoliations"][mwg,MaxItems->5,"BundleFoliations"->True];
It is hard to visualize them nicely, but it’s still something:
In[]:=
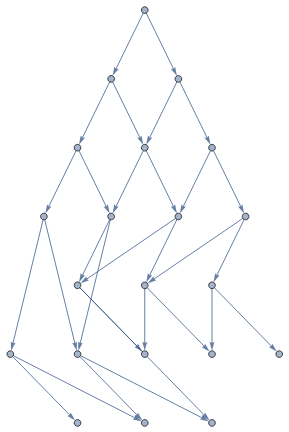
ResourceFunction["LayeredLayoutGraph"][mwg,#]&/@foliations
Out[]=
,
,
,
,
In[]:=
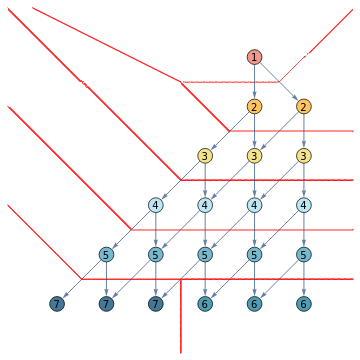
FoliationDiagram[mwg,#,PlotPoints->200]&/@foliations
Out[]=
,
,
,
,
Generate branchial slices for each foliation:
In[]:=
branchialGraphs=branchialGraphList[mwg,#]&/@foliations;
In[]:=
Grid[branchialGraphs,Frame->All]
Out[]=
For each state count the number of edges (completions) in the corresponding slice and the time step of its generation:
In[]:=
stateTimeCompletions=MapIndexed[AssociationThread[VertexList[#],<|"TimeStep"->First[#2],"NumberOfCompletions"->EdgeCount[#]|>]&,#]&/@branchialGraphs
Out[]=
{{AABTimeStep1,NumberOfCompletions1,ABATimeStep1,NumberOfCompletions1,AABBTimeStep2,NumberOfCompletions2,ABABTimeStep2,NumberOfCompletions2,ABBATimeStep2,NumberOfCompletions2,AABBBTimeStep3,NumberOfCompletions3,ABABBTimeStep3,NumberOfCompletions3,ABBABTimeStep3,NumberOfCompletions3,ABBBATimeStep3,NumberOfCompletions3,AABBBBTimeStep4,NumberOfCompletions4,ABABBBTimeStep4,NumberOfCompletions4,ABBABBTimeStep4,NumberOfCompletions4,ABBBABTimeStep4,NumberOfCompletions4,ABBBBATimeStep4,NumberOfCompletions4,ABBBABBTimeStep5,NumberOfCompletions2,ABBBBABTimeStep5,NumberOfCompletions2,ABBBBBATimeStep5,NumberOfCompletions2,},{AABTimeStep1,NumberOfCompletions1,ABATimeStep1,NumberOfCompletions1,AABBTimeStep2,NumberOfCompletions2,ABABTimeStep2,NumberOfCompletions2,ABBATimeStep2,NumberOfCompletions2,AABBBTimeStep3,NumberOfCompletions3,ABABBTimeStep3,NumberOfCompletions3,ABBABTimeStep3,NumberOfCompletions3,ABBBATimeStep3,NumberOfCompletions3,ABBABBTimeStep4,NumberOfCompletions2,ABBBABTimeStep4,NumberOfCompletions2,ABBBBATimeStep4,NumberOfCompletions2,ABBBABBTimeStep5,NumberOfCompletions2,ABBBBABTimeStep5,NumberOfCompletions2,ABBBBBATimeStep5,NumberOfCompletions2,ABABBBBTimeStep6,NumberOfCompletions1,ABBABBBTimeStep6,NumberOfCompletions1},{AABTimeStep1,NumberOfCompletions1,ABATimeStep1,NumberOfCompletions1,AABBTimeStep2,NumberOfCompletions2,ABABTimeStep2,NumberOfCompletions2,ABBATimeStep2,NumberOfCompletions2,AABBBTimeStep3,NumberOfCompletions3,ABABBTimeStep3,NumberOfCompletions3,ABBABTimeStep3,NumberOfCompletions3,ABBBATimeStep3,NumberOfCompletions3,ABABBBTimeStep4,NumberOfCompletions3,ABBABBTimeStep4,NumberOfCompletions3,ABBBABTimeStep4,NumberOfCompletions3,ABBBBATimeStep4,NumberOfCompletions3,ABBBABBTimeStep5,NumberOfCompletions2,ABBBBABTimeStep5,NumberOfCompletions2,ABBBBBATimeStep5,NumberOfCompletions2,AABBBBBTimeStep6,NumberOfCompletions1,ABABBBBTimeStep6,NumberOfCompletions1},{AABTimeStep1,NumberOfCompletions1,ABATimeStep1,NumberOfCompletions1,AABBTimeStep2,NumberOfCompletions2,ABABTimeStep2,NumberOfCompletions2,ABBATimeStep2,NumberOfCompletions2,AABBBTimeStep3,NumberOfCompletions3,ABABBTimeStep3,NumberOfCompletions3,ABBABTimeStep3,NumberOfCompletions3,ABBBATimeStep3,NumberOfCompletions3,ABBABBTimeStep4,NumberOfCompletions2,ABBBABTimeStep4,NumberOfCompletions2,ABBBBATimeStep4,NumberOfCompletions2,ABBBABBTimeStep5,NumberOfCompletions2,ABBBBABTimeStep5,NumberOfCompletions2,ABBBBBATimeStep5,NumberOfCompletions2,AABBBBBTimeStep6,NumberOfCompletions2,ABABBBBTimeStep6,NumberOfCompletions2,ABBABBBTimeStep6,NumberOfCompletions2},{AABTimeStep1,NumberOfCompletions1,ABATimeStep1,NumberOfCompletions1,AABBTimeStep2,NumberOfCompletions2,ABABTimeStep2,NumberOfCompletions2,ABBATimeStep2,NumberOfCompletions2,ABABBTimeStep3,NumberOfCompletions2,ABBABTimeStep3,NumberOfCompletions2,ABBBATimeStep3,NumberOfCompletions2,ABBABBTimeStep4,NumberOfCompletions2,ABBBABTimeStep4,NumberOfCompletions2,ABBBBATimeStep4,NumberOfCompletions2,AABBBBTimeStep5,NumberOfCompletions3,ABABBBTimeStep5,NumberOfCompletions3,ABBBABBTimeStep5,NumberOfCompletions3,ABBBBABTimeStep5,NumberOfCompletions3,ABBBBBATimeStep5,NumberOfCompletions3,AABBBBBTimeStep6,NumberOfCompletions2,ABABBBBTimeStep6,NumberOfCompletions2,ABBABBBTimeStep6,NumberOfCompletions2}}
Merge them:
In[]:=
Merge[stateTimeCompletions,Merge[#,Identity]&]
Out[]=
AABTimeStep{1,1,1,1,1},NumberOfCompletions{1,1,1,1,1},ABATimeStep{1,1,1,1,1},NumberOfCompletions{1,1,1,1,1},AABBTimeStep{2,2,2,2,2},NumberOfCompletions{2,2,2,2,2},ABABTimeStep{2,2,2,2,2},NumberOfCompletions{2,2,2,2,2},ABBATimeStep{2,2,2,2,2},NumberOfCompletions{2,2,2,2,2},AABBBTimeStep{3,3,3,3},NumberOfCompletions{3,3,3,3},ABABBTimeStep{3,3,3,3,3},NumberOfCompletions{3,3,3,3,2},ABBABTimeStep{3,3,3,3,3},NumberOfCompletions{3,3,3,3,2},ABBBATimeStep{3,3,3,3,3},NumberOfCompletions{3,3,3,3,2},AABBBBTimeStep{4,5},NumberOfCompletions{4,3},ABABBBTimeStep{4,4,5},NumberOfCompletions{4,3,3},ABBABBTimeStep{4,4,4,4,4},NumberOfCompletions{4,2,3,2,2},ABBBABTimeStep{4,4,4,4,4},NumberOfCompletions{4,2,3,2,2},ABBBBATimeStep{4,4,4,4,4},NumberOfCompletions{4,2,3,2,2},ABBBABBTimeStep{5,5,5,5,5},NumberOfCompletions{2,2,2,2,3},ABBBBABTimeStep{5,5,5,5,5},NumberOfCompletions{2,2,2,2,3},ABBBBBATimeStep{5,5,5,5,5},NumberOfCompletions{2,2,2,2,3},ABABBBBTimeStep{6,6,6,6},NumberOfCompletions{1,1,2,2},ABBABBBTimeStep{6,6,6},NumberOfCompletions{1,2,2},AABBBBBTimeStep{6,6,6},NumberOfCompletions{1,2,2}