374 Note for Chapter 4: How to find a Wronskian of {f1, f2, ... , fn}, using Mathematica
374 Note for Chapter 4: How to find a Wronskian of {f1, f2, ... , fn}, using Mathematica
Define the functions:
In[]:=
f1[x_]:=E^xf2[x_]:=Sin[x]f3[x_]:=Cos[x]
Make an n x n matrix of functions whose ith row contains the (i-1)st derivatives of {f1, f2, ... , fn}.
A= {f1[x],f2[x],f3[x]}, {f1'[x],f2'[x],f3'[x]}, {f1''[x],f2''[x],f3''[x]}
Out[]=
{{,Sin[x],Cos[x]},{,Cos[x],-Sin[x]},{,-Sin[x],-Cos[x]}}
x
x
x
Here's how to make A look more like a matrix we are used to seeing:
MatrixForm[A]
Out[]//MatrixForm=
x | Sin[x] | Cos[x] |
x | Cos[x] | -Sin[x] |
x | -Sin[x] | -Cos[x] |
Define the Wronskian of {f1, f2, ... , fn}:
In[]:=
W[x_]:=Det[A]
To compute the Wronskian, which is a function of x, evaluate W at x:
W[x]
Out[]=
-2-2
x
2
Cos[x]
x
2
Sin[x]
Simplify[W[x]]
Out[]=
-2
x
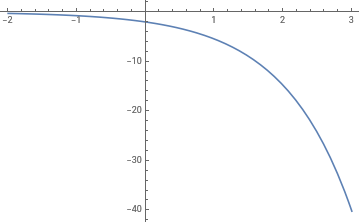
Plot[W[x],{x,-2,3}]
Out[]=
Since the Wronskian is never zero, we conclude that the functions {E^x,Sin[x], Cos[x]} are linearly independent on any real interval!
Here's how to find a Wronskian of 4 functions:
In[]:=
f1[x_]:=1f2[x_]:=xf3[x_]:=x^2f4[x_]:=Cos[x]
B= {f1[x],f2[x],f3[x],f4[x]}, {f1'[x],f2'[x],f3'[x],f4'[x]}, {f1''[x],f2''[x],f3''[x],f4''[x]}, {D[f1[x],{x,3}],D[f2[x],{x,3}],D[f3[x],{x,3}],D[f4[x],{x,3}]}
Out[]=
{{1,x,,Cos[x]},{0,1,2x,-Sin[x]},{0,0,2,-Cos[x]},{0,0,0,Sin[x]}}
2
x
MatrixForm[B]
Out[]//MatrixForm=
1 | x | 2 x | Cos[x] |
0 | 1 | 2x | -Sin[x] |
0 | 0 | 2 | -Cos[x] |
0 | 0 | 0 | Sin[x] |
In[]:=
W1[x_]:=Det[B]
W1[x]
Out[]=
2Sin[x]