166SWC, 7.7 - Example 7: Simpson's (Parabolic) Rule and Error Bounds Discussion
166SWC, 7.7 - Example 7: Simpson's (Parabolic) Rule and Error Bounds Discussion
Recall the Mathematica commands for approximation of f(x)x with or :
b
∫
a
M
n
T
n
In[]:=
MidpointSum[f_,a_,b_,n_]:=f[a+(2*i-1)*(b-a)/(2*n)]*(b-a)/n
n
∑
i=1
In[]:=
Trapezoid[f_,a_,b_,n_]:=(1/2)(f[a+(i-1)*(b-a)/n]+f[a+i*(b-a)/n])*(b-a)/n
n
∑
i=1
1. Construct a command 'Simpson[f_,a_,b_,n_]' that will perform Simpson's rule and compute Sn.
Note that n must be even and Δx=(b-a)/n.
1. Construct a command 'Simpson[f_,a_,b_,n_]' that will perform Simpson's rule and compute .
Note that n must be even and Δx=(b-a)/n.
S
n
Note that n must be even and Δx=(b-a)/n.
2.Testthiscommandontheintegral 1∫0sin(x)xwithn=6andcomparetotheresultswefoundforapproximationsforthisintegralvia𝐿n,𝑅n,𝑀nand𝑇ninExample1.
2.Testthiscommandontheintegral sin(x)xwithn=6andcomparetotheresultswefoundforapproximationsforthisintegralvia,,andinExample1.
1
∫
0
𝐿
n
𝑅
n
𝑀
n
𝑇
n
3. Find an upper bound for using Simpson’s Rule to estimate 1∫0sin(2x)x with even positive integer n. Test this out with n = 10. Here are some ideas that may be useful:
3. Find an upper bound for using Simpson’s Rule to estimate sin()x with even positive integer n. Test this out with n = 10. Here are some ideas that may be useful:
1
∫
0
2
x
To define the function ) with Mathematica, enter the command:
sin(
2
x
In[]:=
f[x_]:=Sin[x^2]
Here is how to find the fourth derivative of f:
f''''[x]
Out[]=
6(-4Cos[]-2Sin[])+2x(-8xCos[]-2x(2Cos[]-4Sin[]))
2
x
2
x
2
x
2
x
2
x
2
x
2
x
If this is too complicated, you can use the 'Simplify' command:
Simplify[%]
Out[]=
-48Cos[]+4(-3+4)Sin[]
2
x
2
x
4
x
2
x
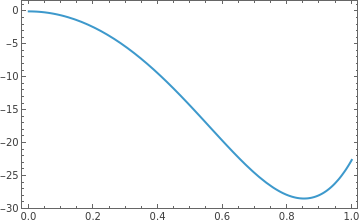
Here is one way to graph f''''[x]:
Plot[f''''[x],{x,0,1},Frame->True]
Out[]=
4.FindthesmallestevenpositiveintegernsothatI-Sn<0.001for2∫-1-2xex.ComparethistowhatwefoundinExamples5and6.
4.FindthesmallestevenpositiveintegernsothatI-<0.001forx.ComparethistowhatwefoundinExamples5and6.
S
n
2
∫
-1
-
2
x
e