166SCW, 7.7 - Example 6: Error Bound Examples Involving Midpoint and Trapezoid Sums
166SCW, 7.7 - Example 6: Error Bound Examples Involving Midpoint and Trapezoid Sums
Recall the Mathematica commands for approximation of f(x)x with or :
b
∫
a
M
n
T
n
In[]:=
MidpointSum[f_,a_,b_,n_]:=f[a+(2*i-1)*(b-a)/(2*n)]*(b-a)/n
n
∑
i=1
In[]:=
Trapezoid[f_,a_,b_,n_]:=(1/2)(f[a+(i-1)*(b-a)/n]+f[a+i*(b-a)/n])*(b-a)/n
n
∑
i=1
Let'slookagainatthedefiniteintegralx.HowlargemustnbetohaveI-<0.001?HowlargemustnbetohaveI-<0.001?
2
∫
-1
-
2
x
e
M
n
T
n
In[]:=
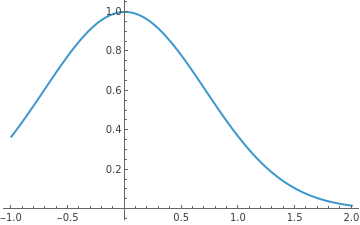
f[x_]:=E^(-x^2)
Plot[f[x],{x,-1,2}]
Out[]=
Equation (5) can be used to determine how large n should be. To apply this equation to estimate the error, we need to bound |f '' (x)| on [-1,2]. Just as before in Example 5, here are two ways to do this:
(i) Graphically:
(i) Graphically:
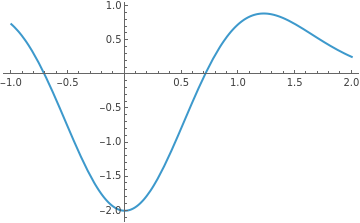
Plot[f''[x],{x,-1,2}]
Out[]=
Clearly,on[-1,2],|f'(x)|≤2,sotake=2inEquation(5).Thenitfollowsthat I-≤,sotaking<0.001>n>
K
2
M
n
2*
3
(2+1)
24*
2
n
2*
3
(2+1)
24*
2
n
2
n
2*
3
(2+1)
24*0.001
2*
3
(2+1)
24*0.001
Sqrt[2*27/(24*.001)]
Out[]=
47.4342
Thus, take n=48.
N[MidpointSum[f,-1,2,48]]
Out[]=
1.62904
Abs[NIntegrate[f[x],{x,-1,2}]-N[MidpointSum[f,-1,2,48]]]
Out[]=
0.00013169
(ii) Using Calculus: On [-1,2], since f '' is continuous, it must attain its maximum and minimum values. These will occur at either endpoints or critical points of f ''.
f'''[x]
Out[]=
8x-2x-2+4
-
2
x
-
2
x
-
2
x
2
x
Solve[f'''[x]==0,x]
Out[]=
{x0},x-,x
3
2
3
2
Sqrt[3./2]
Out[]=
1.22474
Thus, the places where |f ''| can be maximized on [-1,2] are at x=-1, 0, , or x=2:
3/2
Abs[f''[{-1,0,Sqrt[3/2],2}]]
Out[]=
,2,,
2
4
3/2
14
4
N[%]
Out[]=
{0.735759,2.,0.892521,0.256419}
Thus,asabove,weseethat=2,sowegetthesameresultsasbefore!
K
2
For the Trapezoid Sums, using equation (5), an upper bound on the error will be twice as big as that for Midpoint Sums:
I-≤,sotaking<0.001>n>
M
n
2*
3
(2+1)
12*
2
n
2*
3
(2+1)
12*
2
n
2
n
2*
3
(2+1)
12*0.001
2*
3
(2+1)
12*0.001
Sqrt[2*27/(12*.001)]
Out[]=
67.082
This means that we will need to take n = 68 to get an upper bound on the error that is less than 0.001.
N[Trapezoid[f,-1,2,68]]
Out[]=
1.62877
Abs[NIntegrate[f[x],{x,-1,2}]-N[Trapezoid[f,-1,2,68]]]
Out[]=
0.000131225