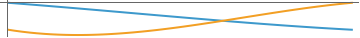Portal frame with fixed column bases and off-center vertical load
Portal frame with fixed column bases and off-center vertical load
Element stiffness matrix
Element stiffness matrix
Depends on the modulus of elasticity, moment of inertia, and length
Axial deformation is ignored
Axial deformation is ignored
In[]:=
ke[EI_,L_]:={{12EI/L^3,6EI/L^2,-12EI/L^3,6EI/L^2},{6EI/L^2,4EI/L,-6EI/L^2,2EI/L},{-12EI/L^3,-6EI/L^2,12EI/L^3,-6EI/L^2},{6EI/L^2,2EI/L,-6EI/L^2,4EI/L}};
Define the structure
Define the structure
Lengths of the members
In[]:=
len={L,L/4,3L/4,L}
Out[]=
L,,,L
L
4
3L
4
Destination array
In[]:=
da={{0,0,1,2},{0,2,3,4},{3,4,0,5},{0,0,1,5}};
In[]:=
nelem=Length[len]
Out[]=
4
In[]:=
nelem==Dimensions[da][[1]](*checkonthenumberofelementsanddarows*)
Out[]=
True
In[]:=
ndof=Max[da]
Out[]=
5
Construct the structural matrices
Construct the structural matrices
Stiffness matrix
In[]:=
k=Table[0,{m,1,ndof},{n,1,ndof}];
In[]:=
Do[Do[If[da[[n,i]]>0&&da[[n,j]]>0,k[[da[[n,i]],da[[n,j]]]]+=ke[EI,len[[n]]][[i,j]]],{i,4},{j,4}],{n,nelem}];
In[]:=
MatrixForm[k]
Out[]//MatrixForm=
24EI 3 L | - 6EI 2 L | 0 | 0 | - 6EI 2 L |
- 6EI 2 L | 20EI L | - 96EI 2 L | 8EI L | 0 |
0 | - 96EI 2 L | 7168EI 9 3 L | - 256EI 3 2 L | 32EI 3 2 L |
0 | 8EI L | - 256EI 3 2 L | 64EI 3L | 8EI 3L |
- 6EI 2 L | 0 | 32EI 3 2 L | 8EI 3L | 28EI 3L |
Load vector
In[]:=
f=Table[0,{n,1,ndof}]
Out[]=
{0,0,0,0,0}
In[]:=
f[[3]]=-P
Out[]=
-P
In[]:=
f
Out[]=
{0,0,-P,0,0}
Structural solution
Structural solution
Displacement vector
In[]:=
u=LinearSolve[k,f]
Out[]=
-,-,-,-,P
3P
3
L
896EI
5P
2
L
224EI
165P
3
L
28672EI
113P
2
L
7168EI
2
L
112EI
Element solutions
Element solutions
Displacement vectors
In[]:=
ue=Table[0,{m,1,nelem},{n,1,4}]
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
In[]:=
Do[Do[If[da[[n,i]]>0,ue[[n,i]]=u[[da[[n,i]]]]],{i,4}],{n,nelem}];
In[]:=
MatrixForm[ue](*eachrowisanelement*)
Out[]//MatrixForm=
0 | 0 | - 3 3 L 896EI | - 5 2 L 224EI |
0 | - 5 2 L 224EI | - 165 3 L 28672EI | - 113 2 L 7168EI |
- 165 3 L 28672EI | - 113 2 L 7168EI | 0 | 2 L 112EI |
0 | 0 | - 3 3 L 896EI | 2 L 112EI |
Force vectors
In[]:=
fe=Table[0,{m,1,nelem},{n,1,4}];
In[]:=
Do[fe[[n]]=ke[EI,len[[n]]].ue[[n]],{n,nelem}];
In[]:=
MatrixForm[fe](*eachrowisanelement*)
Out[]//MatrixForm=
- 3P 32 | - 11LP 448 | 3P 32 | - 31LP 448 |
171P 224 | 31LP 448 | - 171P 224 | 109LP 896 |
- 53P 224 | - 109LP 896 | 53P 224 | - 25LP 448 |
3P 32 | 17LP 448 | - 3P 32 | 25LP 448 |
Plots
Plots
Shape functions; z runs from 0 to 1
In[]:=
shape[L_]:={1-3z^2+2z^3,L(z-2z^2+z^3),3z^2-2z^3,L(-z^2+z^3)}
Beam deflections (elements 2 and 3), full form and normalized
In[]:=
yb={ue[[2]].shape[len[[2]]],ue[[3]].shape[len[[3]]]}
Out[]=
---,-+-
165P(3-2)
3
L
2
z
3
z
28672EI
5P(z-2+)
3
L
2
z
3
z
896EI
113P(-+)
3
L
2
z
3
z
28672EI
339P(z-2+)
3
L
2
z
3
z
28672EI
3P(-+)
3
L
2
z
3
z
448EI
165P(1-3+2)
3
L
2
z
3
z
28672EI
In[]:=
yb=Simplify[yb]
Out[]=
Pz(-160-62z+57),-
3
L
2
z
28672EI
3P(55+113z-327+159)
3
L
2
z
3
z
28672EI
In[]:=
ybn=yb/(PL^3/EI)(*normalized*)
Out[]=
,-
z(-160-62z+57)
2
z
28672
3(55+113z-327+159)
2
z
3
z
28672
In[]:=
Plot[ybn,{z,0,1},AspectRatio->.1,Ticks->None]
Out[]=
In[]:=
Minimize[{ybn[[1]],0≤z≤1},z]
Column deflections (elements 1 and 4 ), full form and normalized
The undisplaced structure
Top corner horizontal displacement, normalized
The multiplier used to magnify the normalized deflections
In[]:=
The displaced structure
Displaced and undisplaced structure