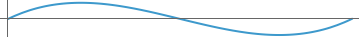Portal frame with fixed column bases and top horizontal load
Portal frame with fixed column bases and top horizontal load
Element stiffness matrix
Element stiffness matrix
Depends on the modulus of elasticity, moment of inertia, and length
Axial deformation is ignored
Axial deformation is ignored
In[]:=
ke[EI_,L_]:={{12EI/L^3,6EI/L^2,-12EI/L^3,6EI/L^2},{6EI/L^2,4EI/L,-6EI/L^2,2EI/L},{-12EI/L^3,-6EI/L^2,12EI/L^3,-6EI/L^2},{6EI/L^2,2EI/L,-6EI/L^2,4EI/L}};
In[]:=
MatrixForm[ke[EI,L]](*easiertoconfirminthisform*)
Out[]//MatrixForm=
12EI 3 L | 6EI 2 L | - 12EI 3 L | 6EI 2 L |
6EI 2 L | 4EI L | - 6EI 2 L | 2EI L |
- 12EI 3 L | - 6EI 2 L | 12EI 3 L | - 6EI 2 L |
6EI 2 L | 2EI L | - 6EI 2 L | 4EI L |
Define the structure
Define the structure
Lengths of the members
In[]:=
len={L,L,L}
Out[]=
{L,L,L}
Destination array
In[]:=
da={{0,0,1,2},{0,2,0,2},{0,0,1,2}};
In[]:=
nelem=Length[len]
Out[]=
3
In[]:=
nelem==Dimensions[da][[1]](*checkonthenumberofelementsanddarows*)
Out[]=
True
In[]:=
ndof=Max[da]
Out[]=
2
Construct the structural matrices
Construct the structural matrices
Stiffness matrix
In[]:=
k=Table[0,{m,1,ndof},{n,1,ndof}];
In[]:=
Do[Do[If[da[[n,i]]>0&&da[[n,j]]>0,k[[da[[n,i]],da[[n,j]]]]+=ke[EI,len[[n]]][[i,j]]],{i,4},{j,4}],{n,nelem}];
In[]:=
MatrixForm[k]
Out[]//MatrixForm=
24EI 3 L | - 12EI 2 L |
- 12EI 2 L | 20EI L |
Load vector
In[]:=
f=Table[0,{n,1,ndof}];
In[]:=
f[[1]]=P
Out[]=
P
In[]:=
f
Out[]=
{P,0}
Structural solution
Structural solution
Displacement vector
In[]:=
u=LinearSolve[k,f]
Out[]=
,P
5P
3
L
84EI
2
L
28EI
Element solutions
Element solutions
Displacement vectors
In[]:=
ue=Table[0,{m,1,nelem},{n,1,4}]
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0}}
In[]:=
Do[Do[If[da[[n,i]]>0,ue[[n,i]]=u[[da[[n,i]]]]],{i,4}],{n,nelem}];
In[]:=
MatrixForm[ue](*eachrowisanelement*)
Out[]//MatrixForm=
0 | 0 | 5 3 L 84EI | 2 L 28EI |
0 | 2 L 28EI | 0 | 2 L 28EI |
0 | 0 | 5 3 L 84EI | 2 L 28EI |
Force vectors
In[]:=
fe=Table[0,{m,1,nelem},{n,1,4}];
In[]:=
Do[fe[[n]]=ke[EI,len[[n]]].ue[[n]],{n,nelem}];
In[]:=
MatrixForm[fe](*eachrowisanelement*)
Out[]//MatrixForm=
- P 2 | - 2LP 7 | P 2 | - 3LP 14 |
3P 7 | 3LP 14 | - 3P 7 | 3LP 14 |
- P 2 | - 2LP 7 | P 2 | - 3LP 14 |
Plots
Plots
Shape functions; z runs from 0 to 1
In[]:=
shape[L_]:={1-3z^2+2z^3,L(z-2z^2+z^3),3z^2-2z^3,L(-z^2+z^3)}
Beam deflection (element2), full form and normalized
In[]:=
yb=ue[[2]].shape[len[[2]]]
Out[]=
3
L
2
z
3
z
28EI
3
L
2
z
3
z
28EI
In[]:=
yb=Simplify[yb]
Out[]=
3
L
2
z
28EI
In[]:=
ybn=yb/(PL^3/EI)(*normalized*)
Out[]=
1
28
2
z
In[]:=
Plot[ybn,{z,0,1},AspectRatio->.1,Ticks->None]
Out[]=
In[]:=
Minimize[{ybn,0≤z≤1},z]//N
Out[]=
{-0.00343661,{z0.788675}}
In[]:=
Maximize[{ybn,0≤z≤1},z]//N
Column deflections (elements 1 and 3 ), full form and normalized
The undisplaced structure
Top corner horizontal displacement, normalized
The multiplier used to magnify the normalized deflections
In[]:=
The displaced structure
Displaced and undisplaced structure