Equation of time

A location on the prime meridian.
In[]:=
prime=GeoPosition[{51.5,0}]
Out[]=
GeoPosition[{51.5,0}]
Define the date range of the plot.
In[]:=
dstart=DateObject[{2025,1,1,12,0},TimeZone->0];​​dend=DateObject[{2025,12,31,12,0},TimeZone->0];
In[]:=
noon=DateRange[dstart,dend];
The offset comes from the Sun position (right ascension) and the sidereal time.
In[]:=
sunpos=Map[SunPosition[prime,#,CelestialSystem"Equatorial"][[1]]&,noon];
In[]:=
stime=Map[UnitConvert[SiderealTime[prime,#],"HoursOfRightAscension"]&,noon];
There are jumps in sunpos and stime because the values can’t be larger than 24 hrs.
In[]:=
ListPlot[sunpos]
Out[]=
50
100
150
200
250
300
350
5
10
15
20
25
In[]:=
ListPlot[stime]
Out[]=
50
100
150
200
250
300
350
5
10
15
20
25
These can cause problems when we take the difference. We fix them by finding the jumps and lowering the values before them.
In[]:=
sunjump=Reverse[Flatten[Position[Differences[QuantityMagnitude[sunpos]],_?Negative]]]
Out[]=
{78}
In[]:=
Do[sunpos[[;;sunjump[[i]]]]=sunpos[[;;sunjump[[i]]]]-Quantity[24,"HoursOfRightAscension"],{i,Length[sunjump]}]
In[]:=
timejump=Reverse[Flatten[Position[Differences[QuantityMagnitude[stime]],_?Negative]]]
Out[]=
{80}
In[]:=
Do[stime[[;;timejump[[i]]]]=stime[[;;timejump[[i]]]]-Quantity[24,"HoursOfRightAscension"],{i,Length[timejump]}]
In[]:=
ListPlot[{sunpos,stime}]
Out[]=
50
100
150
200
250
300
350
-5
5
10
15
20
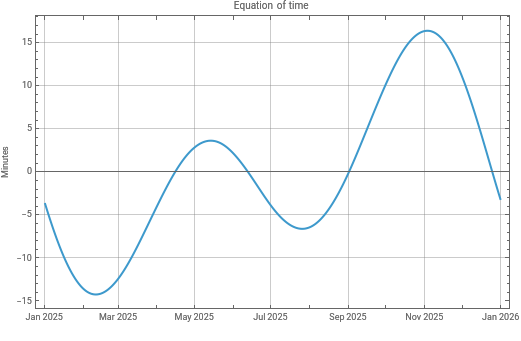
Now we can plot the offset. Solar time is ahead of standard time when the offset is positive.
In[]:=
offset=UnitConvert[stime-sunpos,"MinutesOfRightAscension"];
In[]:=
DateListPlot[Transpose[{noon,offset}],Axes->True,GridLines->Automatic,PlotLabel->"Equation of time",FrameLabel->{"","Minutes"}]
Out[]=