“Equation of time” for Naperville
“Equation of time” for Naperville
Strictly speaking, the equation of time is for the prime meridian, but we can plot the offset of solar time from standard time for any point on the globe.
The location of Nichols Library in Naperville
In[]:=
nichols=GeoPosition[{41.772300,-88.151898}]
Out[]=
GeoPosition[{41.7723,-88.1519}]
Define the range of the plot
In[]:=
dstart=DateObject[{2025,7,1,12,0},TimeZone->-6];dend=DateObject[{2026,6,30,12,0},TimeZone->-6];
In[]:=
noon=DateRange[dstart,dend];
The offset comes from the Sun position (right ascension) and the sidereal time
In[]:=
sunpos=Map[SunPosition[nichols,#,CelestialSystem"Equatorial"][[1]]&,noon];
In[]:=
stime=Map[UnitConvert[SiderealTime[nichols,#],"HoursOfRightAscension"]&,noon];
There are jumps in sunpos and stime because the values can’t be larger than 24 hrs
In[]:=
ListPlot[sunpos]
Out[]=
In[]:=
ListPlot[stime]
Out[]=
These can cause problems when we take the difference. We fix them by finding the jumps and lowering the values before them.
In[]:=
sunjump=Reverse[Flatten[Position[Differences[QuantityMagnitude[sunpos]],_?Negative]]]
Out[]=
{262}
In[]:=
Do[sunpos[[;;sunjump[[i]]]]=sunpos[[;;sunjump[[i]]]]-Quantity[24,"HoursOfRightAscension"],{i,Length[sunjump]}]
In[]:=
timejump=Reverse[Flatten[Position[Differences[QuantityMagnitude[stime]],_?Negative]]]
Out[]=
{262}
In[]:=
Do[stime[[;;timejump[[i]]]]=stime[[;;timejump[[i]]]]-Quantity[24,"HoursOfRightAscension"],{i,Length[timejump]}]
In[]:=
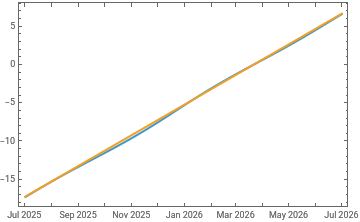
DateListPlot[{Transpose[{noon,sunpos}],Transpose[{noon,stime}]}]
Out[]=
Now we can plot the offset. Solar time is ahead of standard time when the offset is positive.
In[]:=
offset=UnitConvert[stime-sunpos,"MinutesOfRightAscension"];
In[]:=
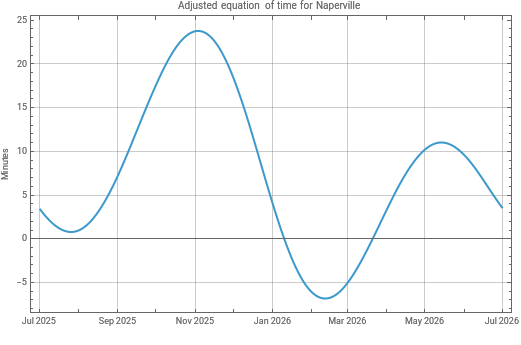
DateListPlot[Transpose[{noon,offset}],Axes->True,GridLines->Automatic,PlotLabel->"Adjusted equation of time for Naperville",FrameLabel->{"","Minutes"}]
Out[]=