Example given in the Lecture on Jan. 19th.Let X and Y be two N(0,1) random variables. The Covarance of X and Y is given byE[X Y] = Sin[π/2 E[Sign[X] Sign[Y]]]The proof relies on the following integral∫_0^2π Sign[Cos[θ]] Sign[Sin[θ+θ_0]] d θBy Le Chen.Crated on Thu Jan 19 08:45:16 PM EST 2023
θ0takestherange-π2,π2
takestherange,
θ
0
-π
2
π
2
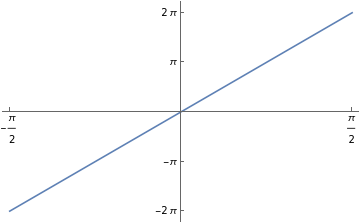
In[]:=
PlotNIntegrate[Sign[Cos[θ]]Sign[Sin[θ+]],{θ,0,2π}],,,,Ticks,0,,{-2π,-π,0,π,2π}
θ
0
θ
0
-π
2
π
2
-π
2
π
2
Out[]=
Plotofonalargerrange[-2π,2π]
θ
0
In[]:=
PlotNIntegrate[Sign[Cos[θ]]Sign[Sin[θ+]],{θ,0,2π}],{,-2π,2π},Ticks-2π,-,-π,,0,,π,,2π,{-2π,-π,0,π,2π}
θ
0
θ
0
3π
2
-π
2
π
2
3π
2
Out[]=