MAM2046W - Second year nonlinear dynamics

Section 3.5: Coupled oscillators and quasiperiodicity

​
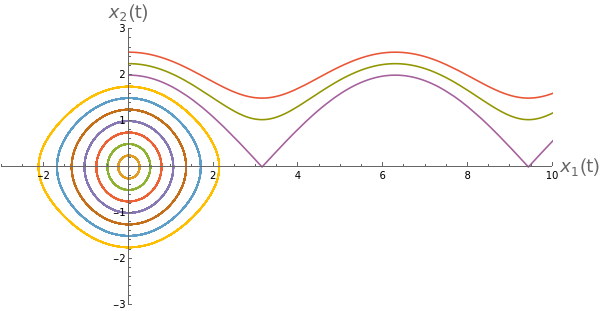
When we discussed the phase space of the pendulum in first year, we said that we were free to choose
θ(0)
and

θ
(0)
, which is indeed true, but we ended up plotting trajectories in phase space like:
In[]:=
xsol[t_,xv_]:=Module[{},sol=NDSolve[{x''[t]+Sin[x[t]]0,x[0]0,x'[0]xv},x,{t,0,100}][[1]];​​{x[t],x'[t]}/.sol];​​ParametricPlot[Evaluate[xsol[t,#]&/@Range[0,2.5,0.25]],{t,0,100},PlotRange->{{-3,10},{-3,3}},AspectRatio->1/2,AxesLabel->{Style["
x
1
​(t)",18],Style["
x
2
​(t)",18]},ImageSize->600]​​
Out[]=
(where here
x
1
isθ
and
x
2
is

θ
). We never took into account the fact that θ is periodic (though

θ
is of course not) - ie
θ+2πisidentifiedwithθ
. The way we should do this is to acknowledge that the phase plane shouldn’t be
2

but it should be
1

×
1
S
- ie a cylinder.
In[]:=
xsol[t_,xv_]:=Module[{},sol=NDSolve[{x''[t]+Sin[x[t]]0,x[0]0,x'[0]xv},x,{t,0,100}][[1]];​​{x[t],x'[t]}/.sol];​​Evaluate[xsol[t,#]&/@Range[0,2.5,0.25]];​​TableParametricPlot3D[Evaluate[{Cos[#[[1]]],Sin[#[[1]]],#[[2]]}&/@%],{t,0,100},ViewPointRotationTransform[θ,{0,0,1}][{3,0,1}]],θ,0,2π,
2π
20
;​​ListAnimate[%,SaveDefinitions->True,AnimationRunTime->10]
Out[]=
Imagine taking the first plot and pasting it around a cylinder of circumference 2π.
​
OK, so here we have an example when a phase plane is most naturally described as a phase cylinder. Are there other systems for which we might have a different description?
​
We know that in a one dimensional system we can’t have any oscillations in terms of a back and forth motion, but of course we can have a flow on the line, where there is an identification on the line meaning that it’s really on a circle. Such a flow would be given by:

θ
=f(θ)withidentificationθ+2π∼θ
where the ∼ symbol means “is identified with”. This is really a flow on a circle.
​
We can do the same thing in two dimensions, and think about having two coupled oscillators (flows on a circle), given by, for instance

θ
1
=
ω
1
+
K
1
sin(
θ
2
-
θ
1
)

θ
2
=
ω
2
+
K
2
sin(
θ
1
-
θ
2
)
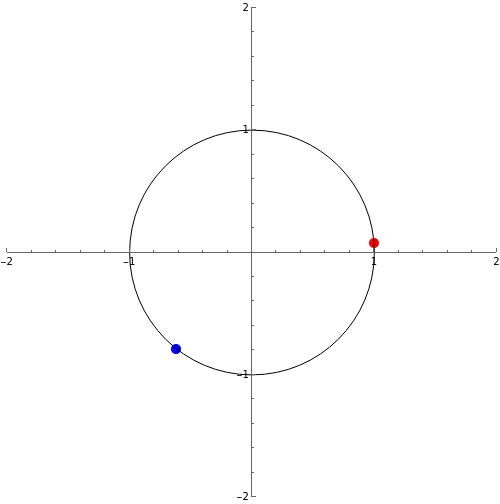
Where
ω
1
and
ω
2
are
the natural frequencies of the motion (ie. without the
K
i
terms
we would just have
θ
i
going
around a circle at frequency
ω
i
), and
K
i
are
coupling constants. We see then that when
θ
1
and
θ
2
are very close to each other, or differ by π, the couplings are small, and when they differ by
π
2
or
3π
2
the couplings are large. This system wants to keep the
θ
i
closeto
each other, or exactly out of phase. Both the
θ
i
live
on a circle. We can plot them on the same circle and see their trajectory. For instance if we start with
ω
1
=1
,
ω
2
=5
and both
K
i
=1
we get:
In[]:=
{θ1[t],θ2[t]}/.NDSolve[{θ1'[t]==1+Sin[θ2[t]-θ1[t]],θ2'[t]==5+Sin[θ1[t]-θ2[t]],θ1[0]==0,θ2[0]==0.5},{θ1,θ2},{t,0,20}][[1]];​​Table[Show[ListPlot[Evaluate[Evaluate[{{Sin[%[[#]]],Cos[%[[#]]]}}]],PlotRange->{{-2,2},{-2,2}},PlotStyle->{{Red,PointSize[0.02]},{Blue,PointSize[0.02]}}[[#]]]&/@{1,2},Graphics[Circle[{0,0},1]],ImageSize->500,AspectRatio->1],{t,0,3,0.1}];​​ListAnimate[%,SaveDefinitions->True]​​
Out[]=
Is there a simpler way that we could illustrate this? We normally like to think about the state of a system as a single point in phase space. The problem with the above is that we have a single state as being given by two points on the circle. The issue is that we have a two dimensional phase space and we are trying to represent it on a one dimensional space. So what we really need is a space with two compact directions. Such a space is the torus. In the above, we have a state given by two points
(
θ
1
(t),
θ
2
(t)).
The torus is a surface which is parameterised by
(
θ
1
(t),
θ
2
(t)).
So for two points on the circle corresponds to a single point on the surface of the torus.
​
The torus is actually given by the product space
1
S
×
1
S
, which is like having two independent circles. One way to see this is to take a piece of paper and first identify the left and right opposite sides. You’ve now got one circular direction. Now do the same thing with the top and bottom (actually, this will be hard with paper as it’s not stretchable) and you have two circular directions.
​
Taking the above system of two positions on the circle
(
θ
1
,
θ
2
)and
converting them to one position on the torus, we get the following trajectory:
​
In[]:=
{θ1[t],θ2[t]}/.NDSolve[{θ1'[t]==1+Sin[θ2[t]-θ1[t]],θ2'[t]==5+Sin[θ1[t]-θ2[t]],θ1[0]==0,θ2[0]==0.5},{θ1,θ2},{t,0,20}][[1]];​​Table[Show[ParametricPlot3D[{Cos[t](2+Cos[u]),Sin[t](2+Cos[u]),Sin[u]},​​{t,0,2Pi},{u,0,2Pi},PlotStyle->Opacity[0.5],​​PlotRange->All,Mesh->False],ListPointPlot3D[{{Cos[%[[2]]](2+Cos[%[[1]]]),Sin[%[[2]]](2+Cos[%[[1]]]),Sin[%[[1]]]}}/.t->t1,PlotStyle->Blue],ParametricPlot3D[{Cos[%[[2]]](2+Cos[%[[1]]]),Sin[%[[2]]](2+Cos[%[[1]]]),Sin[%[[1]]]}/.t->t2,{t2,0,t1},PlotStyle->Red]],{t1,0.1,10,1}];​​ListAnimate[%,SaveDefinitions->True]
Out[]=
​
This particular case is an example of a general form of a vector field which lives on a torus. That of
​
​
Going back to the coupled oscillator, there are a couple of interesting limits we can look in.
​
The first is to ask what happens if the system is not coupled at all. Well, then we get two particles moving around the circle at their own rate, say 1:
​
Clearly if they are both moving at the same rate, then not only is each particle's trajectory periodic with period 2π, but in fact after 2π, the whole system is back to where it started. How about where we have
well, here, although the first has period π and the second has period 2π, it takes 2π for the whole system to get back to where it started, although the first oscillator has been around twice by this point. What about if we had
​
​
Plotting this on the torus we see:
The path that the trajectory makes on the torus is the so-called trefoil knot, which, if we turn the trajectory into a tube to make it easier to visualise, looks like:
In fact we can make a more general statement. If we have two frequencies
​
Somehow we have a system where the natural frequency is given by the difference between the original frequencies, and the new “coupling” is additive in the old couplings.
​
​
What do we do when we are looking at dynamical systems? We ask about the fixed points! The fixed points are clearly given by
Well, this only has solutions when
In fact there will be exactly two fixed points for
and only one when
​
Which looks very much look a saddlenode bifurcation...I rephrase...it is a saddlenode bifurcation.
​
Thankfully both give the same frequency of
we have the following trajectories
If we have
then there is no fixed point, and no phase locking. You can see here that the lines keep crossing each other.
The boundary between the phase locked dynamics and the non phased locked dynamics is a saddlenode bifurcation of cycles.
​
​
Next Page
​
Homepage