Section 3.6: An Aside - Chaos and the Logistic Map.
Section 3.6: An Aside - Chaos and the Logistic Map.
Chaos and the Logistic Map
Let’s take a bit of a break from these bifurcations of first order differential equations and look at another situation where we get some very very interesting behaviour with fixed points. I’ve mentioned it briefly before, but let’s go into some more detail. We’re going to be looking at not a differential equation, but a difference equation. This one is called The Logistic Map:
P
n
P
n-1
P
n-1
We can think of this as a population on a given day (or week, or year, or whatever), and is some sort of growth rate. It is related to the population at the previous time step. Let’s say , if the population at time-step 0 is 0.2, then on the next time step, the population will be:
r
r=2
P
1
So the population has grown. How about the next time step?
P
2
We can write a piece of code which calculates the population through time for a given initial population and value of :
r
In[]:=
ClearAll["Global`*"]
In[]:=
(*Herepnisandpnm1is*)createplot[p0_,r_,timesteps_]:=Module[{},pn[pnm1_]=rpnm1(1-pnm1);populationlist=Partition[Riffle[Range[0,timesteps-1],NestList[pn,p0,timesteps]],2];ListPlot[populationlist,AxesLabel{Style["n",14],Style["",14]},JoinedTrue,MeshAll,PlotLabelStyle[" = "<>ToString[p0]<>", r = "<>ToString[r],16],PlotRangeAll]]createplot[0.2,2,10]
p
n
p
nm1
P
n
P
0
Out[]=
Let’s look at it with, a higher starting population:
In[]:=
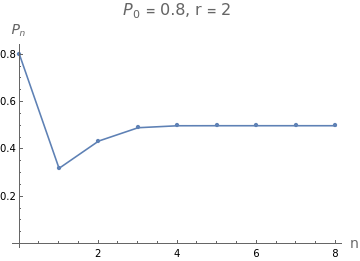
createplot[0.8,2,10]
Out[]=
We see that starting at 0.8, the population first plummets, then it starts to go up again.
Exercise: Try and code this up yourself in Python.
If we start even higher, then something funky happens:
In[]:=
createplot[1.2,2,10]
Out[]=
This looks bad! We seem to end up with a negative population. Well, while this doesn’t make sense in terms of a population, it still makes sense in terms of the equation. If we have a population greater than 1 at any time, then the next time step we will have a negative population, and once you have that, it will keep decreasing infinitely. So anything starting with a population of greater than 1 or less than 0 will end up flying off to -∞.
Let’s look at a range of starting values between 0 and 1:
In[]:=
Manipulate[Show[createplot[p0,2,10],PlotRange{-0.1,1.1},PlotLabel" = "<>ToString[p0]<>", r=2",AxesOrigin{0,0}],{{p0,0.8},0,1,0.1},SaveDefinitions->True]
P
0
Out[]=
We see that there are two fixed points here. One at 0, which is reached when you either start with =0, or =1, and another one. A fixed point is defined by = and so they can be found by solving:
P
0
P
0
P
n
P
n-1
P
n
P
n
P
n
Re-arranging this gives us:
P
n
P
n
r-1
r
which for the case of gives 0 and 0.5. What happens as we decrease ?
r=2
r
In[]:=
Manipulate[Show[createplot[p0,1.5,10],PlotRange{-0.1,1.1},PlotLabel" = "<>ToString[p0]<>", r=1.5",AxesOrigin{0,0}],{{p0,0.8},0,1,0.1},SaveDefinitions->True]
P
0
Out[]=
For the second fixed point seems to have moved down a bit. Let's see what happens as we continue to alter :
r=1.5
r
In[]:=
Manipulate[Show[createplot[p0,r,10],PlotRange{-0.1,1.1},PlotLabel" = "<>ToString[p0]<>", r = "<>ToString[r],AxesOrigin{0,0}],{{p0,0.8},0,1},{{r,1.5},0,2,0.1},SaveDefinitions->True]
P
0
Out[]=
How on Earth could we find anything interesting in the humble Logistic Map equation?
Something strange is about to happen...
Let's write down two equations:
This has four solutions:
Explore what happens if you start close to the true, but unstable fixed point.
This going from one to two to four values that we jump between is known as period doubling.
What the...!?!? Has something gone wrong with our program?
That seems pretty different... Let’s actually zoom into a region between 3.6 and 3.61...
The strange thing is that within this chaos we see an island of calm, between around 3.605 and 3.6065. And indeed within the chaos you will keep seeing islands of calm.
Exercise: Explore this with Python.
What has this got to do with the real world? Well, it turns out that a lot if not most of what is around you is part of a chaotic system!
and this number appears all over nature in systems that become chaotic.
Mathemafrica: Mandelbrot set.
Have a look at this blog-post:
to learn more about Feigenbaum and his constant.
I’m going to leave you with this plot. See if you can figure out what’s going on. The red line is a line of gradient 1 through the origin:
Back to our study of first order differential equations!