Wolfram Cloud Document

WOLFRAM NOTEBOOK

Section 1.5: The Spectrum of Systems of Differential Equations

The Spectrum of Systems of Differential Equations

There are many different families of dynamical systems, from the simplest, to the most complex. We’ve said that a dynamical system can be written in the form:

'(t)=

(

(t),

(t),...,

(t))

'(t)=

(

(t),

(t),...,

(t))

....

'(t)=

(

(t),

(t),...,

(t))

Clearly if there is just one variable

that’s about as simple as you can get. It turns out that there are systems where there are not just a lot of different

but an infinite number. One treats these not as discrete systems, but so called continuous systems.

There's a very important area of physics called quantum field theory, where one can describe the world using an infinite number of interacting

. We will NOT deal with this in this course!

Another classification is given by the types of functions

. The two options are linear functions, and non-linear functions. For a system of linear differential equations, the functions on the right are all simply linear functions of the

For instance:

'(t)=5+

(t)+4

(t)

'(t)=-

(t)-

(t)

The terms on the right are either of zeroth order in the

or first order. There are no terms with for instance

(

)

sin(x)

or the like. If there are constant terms (as in the 5, in equation 0.4 above), then these are known as inhomogeneous. If every term is precisely of first order in the

then it is a homogenous equation.

It turns out that systems of linear first order differential equations are always possible to solve. The most complex behaviour however tends to happen when we have non-linear differential equations - ie. where the

are anything but linear.

That being said, we are going to be able to take non-linear systems and discover certain properties of them by approximating them in clever ways as linear systems.

I've produced a table here which is highly inspired by that in the book by Strogatz, but with some of my own thoughts thrown in too. You don’t need to know this table specifically, but notice how the cases show up in your respective courses (not only this one).

N is the number of differential equations in the system.

System	Linear	N	Chaotic	Image	Notes
Populationgrowth(exponential)	y	1	n
Populationgrowth(logistic)	n	1	n
Radioactivedecay	y	1	n
Linearisedpendulum	y	2	n		Apendulumwithasmallamplitude
Pendulum	n	2	n
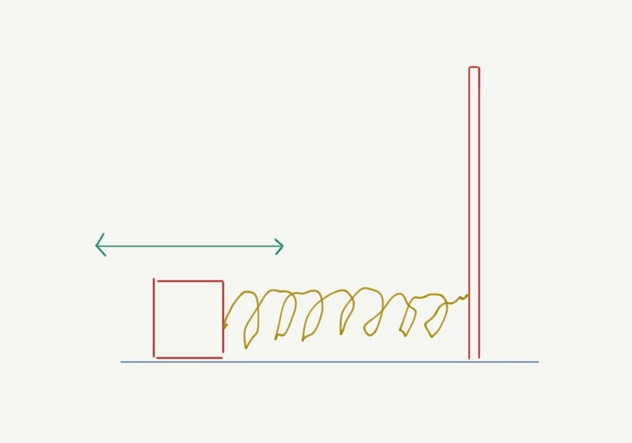
Massonaspring	y	2	n
2-bodyproblem	y	2	n
3-bodyproblem	n	3	y
Strangeattractor	n	3	y
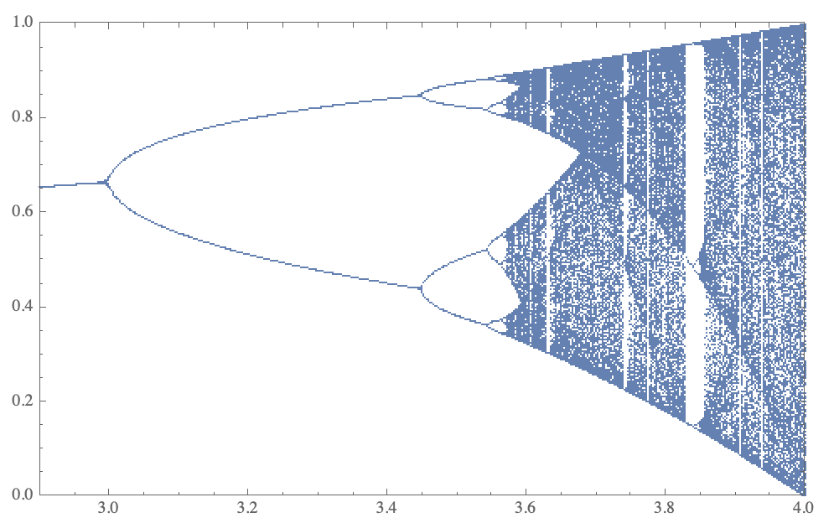
Iteratedmaps	n	3	y
Coupledharmonicoscillators	y	n>>1	n
Solid-statephysics	y	n>>1	n		Seehere.
Laserphysics	n	n>>1	y		Seehere.
Heartcelldynamics	n	n>>1	y
Neuronsinthebrain	n	n>>1	y
Ecosystems	n	n>>1	y
Economics	n	n>>1	y
Waveequations	y	continuum	n
Quantummechanics	y	continuum	n
non-linearwaves	n	continuum	y
Earthquakes	n	continuum	y
QuantumFieldTheory	n	continuum	y
Turbulentfluids	n	continuum	y