Definimos las constantes del problema. Importante tomar α pequeño para que sea válida la aproximación
w1=1;​​w2=1.6;​​α=0.05;​​a=1;​​b=2;​​sol=NDSolve[{x''[t]+w1^2*x[t]-2*α*x[t]*y[t]==0,y''[t]+w2^2*y[t]-α*(x[t])^2==0,x[0]==a,x'[0]==0,y[0]==b,y'[0]==0},{x[t],y[t]},{t,0,50}]
Out[]=
x[t]InterpolatingFunction
Domain: {{0.,50.}}
Output: scalar
[t],y[t]InterpolatingFunction
Domain: {{0.,50.}}
Output: scalar
[t]
In[]:=
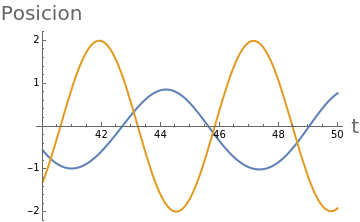
Plot[{Evaluate[x[t]/.sol],Evaluate[y[t]/.sol]},{t,40,50},PlotLegends{Style["x(t)",FontSize15],Style["y(t)",FontSize15]},AxesLabel{Style["t",FontSize20],Style["Posicion",FontSize20]}]
Out[]=
x(t)
y(t)
Comparamos los resultados
In[]:=
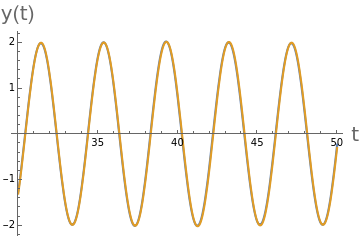
Plot[{a*Cos[w1*t]-α*a*b/(w2*(2*w1+w2))*Cos[(w1+w2)*t]+α*a*b/(w2*(2*w1-w2))*Cos[(w1-w2)*t],Evaluate[x[t]/.sol]},{t,30,50},PlotLegends{Style["Aproximacion",FontSize15],Style["Numerico",FontSize15]},AxesLabel{Style["t",FontSize20],Style["x(t)",FontSize20]}]
Out[]=
Aproximacion
Numerico
In[]:=
Plot[{b*Cos[w2*t]+α*a^2/(2*w2^2)+α*a^2/(2*(w2^2-4*w1^2))*Cos[2*w1*t],Evaluate[y[t]/.sol]},{t,30,50},PlotLegends{Style["Aproximacion",FontSize15],Style["Numerico",FontSize15]},AxesLabel{Style["t",FontSize20],Style["y(t)",FontSize20]}]
Out[]=
Aproximacion
Numerico
In[]:=
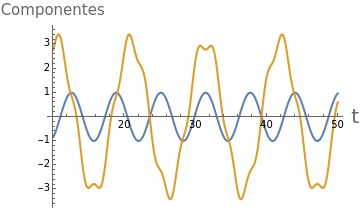
Plot[{a*Cos[w1*t],-a*b/(w2*(2*w1+w2))*Cos[(w1+w2)*t]+a*b/(w2*(2*w1-w2))*Cos[(w1-w2)*t]},{t,10,50},PlotLegends{Style[Superscript["x","(0)"],FontSize15],Style[Superscript["x","(1)"],FontSize15]},AxesLabel{Style["t",FontSize20],Style["Componentes",FontSize15]}]
Out[]=
(0)
x
(1)
x