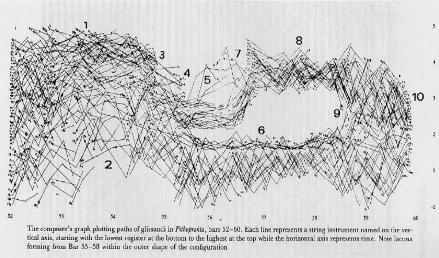
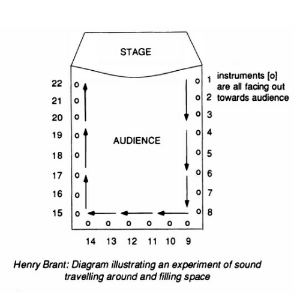
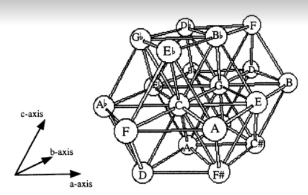
What is the relationship between the arts (inclusive of scifi, music, poetry, and interactive experiences) and research (inclusive of mathematics, physics, and other sciences) ? If it can be termed ‘motivational,’ (i.e. a person discovers a particular topic via a scifi novel and studies it sufficiently much that this person makes a unique and valuable insight into the field), can this degree of motivation be aggregated and quantified? Additionally are there clear examples of an insight or key breakthrough in these fields being stimulated by artistic input (e.g. Einstein’s violin, Von Neumann and Faust, etc.) ? Is there any reliable rule that can used to map these categories of human experience to each other?
Is there one or more sets of harmonics that can be formalized and described mathematically that correspond to intelligence and, by extension, by the growth of complex forms? Can such be derived from physical matter, compositions, or other large data sets? Can such be used to procedurally generate the same?
Is there any formal heuristic that can be used to rank the quality of thoughts? What is the baseline meaningful concept of intuition with respect to selecting “better” thoughts? What makes them better? How did the folk definition of “intuition” evolve into its current format? What are the most useful historical versions of ‘intuition’ and what were their immediate precedents?
To what extent is the quality and meaningful nature of thought related to the complexity of the grammar used to produce it? Specifically does use of nested sub clauses and, by extension, recursion lead to higher quality thought? Can a similar analogy be used for music? Can these be mapped over a time axis such that complexity of grammar or musical phrases is illustrated? If so, can transformer sets or analogous be used to recreate and simulate various versions of the same?