Solution SG 06
Solution SG 06
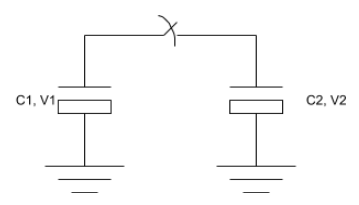
Given two capacitors, each of capacitance C what is the total energy in the capacitors, before (Ei) and after (Ef) closing the switch? The switch is ideal, having no parasitic C, R or L.
(a) Ei = Ef
(b) Ei > Ef
(c) Ei < Ef
(d) 0
(b) Ei > Ef
(c) Ei < Ef
(d) 0
Given C1=C2= C.
The potential (or energy) needed to keep the charges physically separated in the capacitor is the voltage (V) across the capacitor. The initial energy Ei is the sum of the energies in the individual capacitors.
The potential (or energy) needed to keep the charges physically separated in the capacitor is the voltage (V) across the capacitor. The initial energy Ei is the sum of the energies in the individual capacitors.
(1) Ei = V1 + V2
When the switch is closed the capacitors charge share so that the final voltage across the system is V.
(2) Initial charge in C1 is Q1 = C*V1
(3) Iniital charge in C2 is Q2 = C*V2
(3) Iniital charge in C2 is Q2 = C*V2
The sum of the initial charges must equal the final charge in the system; because charge is conserved.
(4) C*(V1+V2) = 2*C*V
(4) C*(V1+V2) = 2*C*V
The total energy in the system is the final voltage, V. Algebraic manipulation of (4) returns V.
(5) V = C*(V1+V2)/(2*C) = 0.5*(V1+V2)
The final energy Ef is the (common) voltage across the capacitors; which is the result in (5).
(6) Ef = 0.5*(V1+V2)
◼
The final energy in the system is smaller than the initial energy.