2020 Solution 07
2020 Solution 07
Isaac Abraham
2020 June 17
2020 June 17
Determine the rms value of v(t) = -0.5 + sin(2π t)
■ The root mean square value of a signal is the DC value that transfers the same energy to the load.
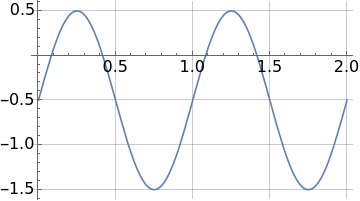
Taking a step-by-step approach, the first step is to visualize the voltage waveform. Let g(x) = -0.5 + sin(ω t).
In[]:=
g[t_]:=-0.5+Sin[2Pi1t]
In[]:=
Plot[g[t],{t,0,2},AxesStyle16,GridLinesAutomatic]
Out[]=
Where are the zeros?
In[]:=
FindRoot[g[t]==0.0,{t,#}]&/@{0,0.5,1}
Out[]=
{{t0.0833333},{t0.416667},{t1.08333}}
With a knowledge of the roots, we can determine the energy in the domains (0.083, 0.417) and (0.417, 1.083); which define a full cycle. Equate the total energy to vrms^2/R; to find vrms.
In[]:=
vrmsRule=Solve[vrms(vrms/1)==Integrate[g[t]^2,{t,0.083,0.417}]+Integrate[g[t]^2,{t,0.417,1.083}],vrms]
Out[]=
{{vrms-0.866025},{vrms0.866025}}
Verify the answer by comparing the energy associated with Vrms (left side of equality) and Vac (right side of equality).
In[]:=
vrmsRule[[2,1,2]]*(vrmsRule[[2,1,2]]/1)*1==Integrate[g[t]^2,{t,0.083,0.417}]+Integrate[g[t]^2,{t,0.417,1.083}]
Out[]=
True