2019 Solution 01
2019 Solution 01
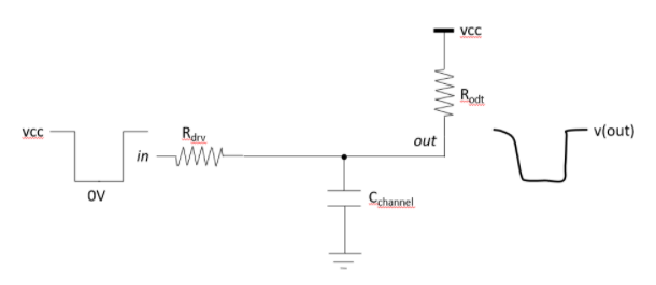
Consider the following circuit topology where the input v(in) transitions Hi-Lo-Hi. Assume Rdrv = Rodt = R.
We make the following two observations.
■ When the input transitions high low the output net discharges through R; with a time constant τ_fall = RC.
■ When the input transitions low high the output net charges through R/2; with a time constant τ_rise = (R/2)C.
■ When the input transitions high low the output net discharges through R; with a time constant τ_fall = RC.
■ When the input transitions low high the output net charges through R/2; with a time constant τ_rise = (R/2)C.
Choose the correct answer.
(a) The reasoning is not right. The correct answer should be τ_rise = τ_fall.
(b) The reasoning is not right. The correct answer should be τ_rise > τ_fall.
(c) The reasoning is right. The correct answer is τ_rise < τ_fall.
(d) The reasoning is right for small C. The correct answer is τ_rise < τ_fall.
(a) The reasoning is not right. The correct answer should be τ_rise = τ_fall.
(b) The reasoning is not right. The correct answer should be τ_rise > τ_fall.
(c) The reasoning is right. The correct answer is τ_rise < τ_fall.
(d) The reasoning is right for small C. The correct answer is τ_rise < τ_fall.
Approach 1
Approach 1
You may have already noticed that when the input transitions H → L, the capacitor discharges through Rdrv. The new reality is that the output voltage is the result of voltage division among the resistors. The output voltage must drop from vcc → 0.5 vcc; which means that a current must also flow in Rodt. Thus both resistors are now “active” making the resistance at out look like R/2. Therefore the correct equation for τ_fall = (R/2) C. Hence (a).
Approach 2
Approach 2
We observe that the net out should satisfy Kirchoff’s Current Law. The tick denotes derivative w.r.t time.
C v(out)' + (2/R) v(out) - vcc/R = v(in)/R
You can solve this numerically or symbolically to arrive at the time constant; remember to use the correct initial conditions.
v(out) = (1/2) exp(-2t/(C*R))*(±1+exp(2t/(C*R)))
You will find that τ_rise = τ_fall. Hence (a).
Approach 3
Approach 3
Approach 3: Create a SPICE model. Simulation and measurement shows that the time constant is equal for rising and falling edges. Hence (a).