2017 Solution 10
2017 Solution 10
Isaac Abraham
2017/09/30
2017/09/30
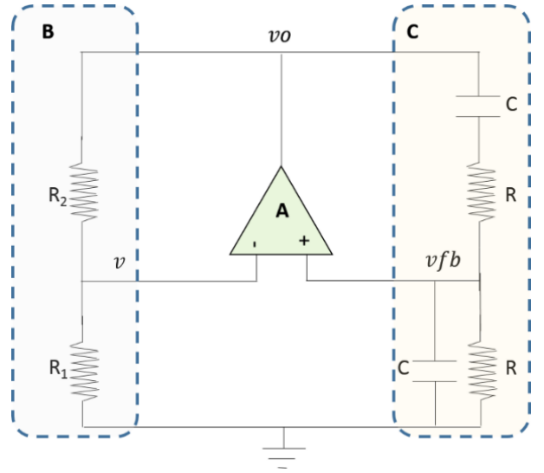
What is the minimum ratio that is required to make the following Wien bridge oscillate?
R
2
R
1
The Wien bridge has two important networks around the opamp. The frequency selector network C on the right hand side sets the frequency of oscillation. Let us define its transfer function as = +.
G
fb
Z
PD
Z
PD
Z
PU
First define the pulldown impedance.
In[]:=
ZPD=R(-/(ωC))/(R-/(ωC));
Next defined the pullup impedance.
In[]:=
ZPU=R-/(ωC);
Calculate the transfer function of the feedback network at the point where it feeds back into the positive input of the opamp.
In[]:=
ZFB=ZPD/(ZPD+ZPU)//.{R1,C1,ω1}
Out[]=
1
3
The feedback network always evaluates to regardless of the values of the components.
1
3
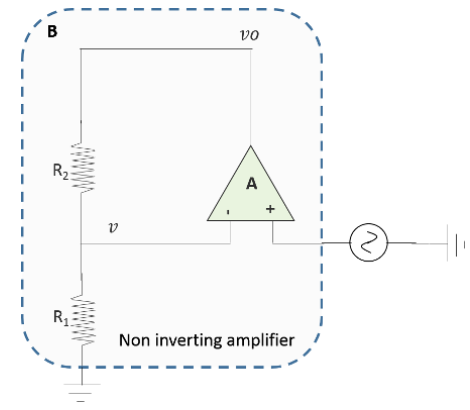
The role of the gain network B on the left hand side is to provide sufficient gain to overcome the attenuation in the frequency selector network. The overall gain required to undo the attenuation is 3. However, we make the observation that the frequency selector is the "signal source"; which makes the entire circuit a non-inverting amplifier.
The gain of a non-inverting amplifier is G= 1+. Therefore = 3-1 = 2.
R
2
R
1
R
2
R
1