Explicación visual del problema Putnam 2025 A3
Explicación visual del problema Putnam 2025 A3
por Shenghui Yang
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “Visual explanation of the problem Putnam 2025 A3” producido con ayuda de un LLM y verificado por un traductor profesional
Problema: Alicia y Bob juegan un juego con una cadena de n dígitos, cada uno de los cuales está restringido a ser 0, 1 o 2. Inicialmente, todos los dígitos son 0.
Un movimiento legal consiste en sumar o restar 1 a un dígito para crear una nueva cadena que no haya aparecido antes. Un jugador que no tenga movimientos legales pierde,
y el otro jugador gana. Alicia comienza, y los jugadores alternan turnos. Para cada n ≥ 1, determine qué jugador tiene una estrategia que garantice la victoria.
Tanto el enunciado como las soluciones están disponibles en https://kskedlaya.org/putnam-archive/.
Un movimiento legal consiste en sumar o restar 1 a un dígito para crear una nueva cadena que no haya aparecido antes. Un jugador que no tenga movimientos legales pierde,
y el otro jugador gana. Alicia comienza, y los jugadores alternan turnos. Para cada n ≥ 1, determine qué jugador tiene una estrategia que garantice la victoria.
Tanto el enunciado como las soluciones están disponibles en https://kskedlaya.org/putnam-archive/.
Juego a grafo
Juego a grafo
Para evitar un exceso de elementos visuales en el grafo de la solución, elijo para la visualización.
n=4
«... un juego con una cadena de n dígitos, cada uno de los cuales está restringido a ser 0, 1 o 2» es equivalente a usar Tuples para generar todos los conjuntos ordenados de 4 elementos excluyendo {0,0,0,0}
In[]:=
nodes=Rest@Tuples[{0,1,2},4];
Cuente el número de nodos:
In[]:=
len=Length[nodes]
Out[]=
80
Cree dos objetos de arreglo dinámico para almacenar los nodos adyacentes. Si dos nodos difieren exactamente en una unidad en una sola posición, dibuje una arista que los conecte; por ejemplo, {1, 1, 2, 1} está vinculado a {2, 1, 2, 1}. En cambio, no se dibuja ninguna arista entre {1, 1, 1, 1} y {2, 2, 2, 2}.
In[]:=
Once[dy1=CreateDataStructure["DynamicArray"];dy2=CreateDataStructure["DynamicArray"];]
In[]:=
dy1["DropAll"];dy2["DropAll"];
In[]:=
Do[With[{res=Abs[nodes[[i]]-nodes[[j]]]},If[Total[res]==1,dy1["Append",nodes[[i]]];dy2["Append",nodes[[j]]];]],{i,1,len-1},{j,i+1,len}]
Cree una lista de aristas para el grafo:
In[]:=
el=Thread[dy1["Elements"]dy2["Elements"]];
Cuente el número de aristas:
In[]:=
Length[el]
Out[]=
212
Visualice el grafo:
In[]:=
g=Graph[el]
Out[]=
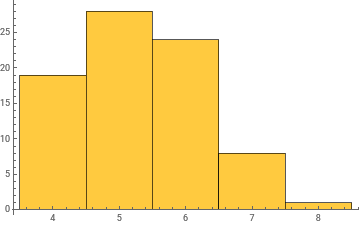
Distribución del grado del vértice:
In[]:=
Histogram[VertexDegree[g]]
Out[]=
Automorfismo y su orden de grupo:
In[]:=
GraphAutomorphismGroup[g]
Out[]=
PermutationGroup[{Cycles[{{4,5},{7,8},{11,12},{14,15},{17,18},{19,20},{21,22},{23,24},{25,53},{26,54},{28,55},{30,56},{32,57},{34,58},{36,59},{38,60},{40,61},{42,62},{44,63},{45,64},{46,65},{47,66},{48,67},{49,68},{50,69},{51,70},{52,71}}],Cycles[{{3,4},{6,7},{9,25},{10,26},{12,27},{13,28},{15,29},{16,30},{18,31},{19,32},{20,44},{21,34},{22,45},{23,36},{24,46},{39,47},{41,48},{43,49},{57,63},{58,64},{59,65},{60,72},{61,73},{62,74},{69,75},{70,76},{71,77}}],Cycles[{{1,9},{2,10},{4,11},{5,12},{6,13},{7,19},{8,20},{17,21},{18,22},{28,32},{29,33},{30,38},{31,39},{36,40},{37,41},{45,47},{46,50},{49,51},{55,57},{56,60},{59,61},{64,66},{65,69},{68,70},{73,75},{74,78},{77,79}}]}]
In[]:=
GroupOrder[%]
Out[]=
24
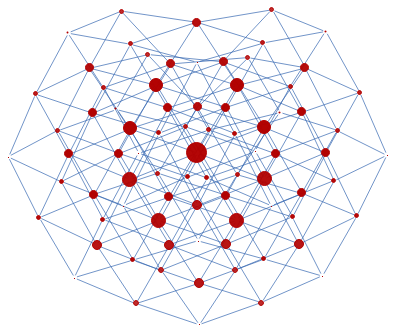
Calcule las centralidades de cercanía y resalte:
In[]:=
HighlightGraph[g,VertexList[g],VertexSize->Thread[VertexList[g]->Rescale[ClosenessCentrality[g]]]]
Out[]=
Emparejamiento perfecto en grafos
Emparejamiento perfecto en grafos
El paso clave para el cálculo es reconocer que el conjunto de emparejamiento perfecto siempre existe para el grafo. Para encontrar el conjunto adecuado, use la siguiente función:
In[]:=
inEset=FindIndependentEdgeSet[el];
Resaltando las aristas de los pares anteriores:
In[]:=
op=Transpose[Outer[#1->#2&,inEset,{Directive[StandardOrange,Thickness[0.01]]}]][[1]];
In[]:=
Graph[el,EdgeStyle->op]
Out[]=
Volvamos a la pregunta original: si Alicia elige cualquier vértice en el grafo, Bob elige el vértice conectado por la línea naranja. Así que Bob tiene una estrategia ganadora.
OEIS A224327
OEIS A224327
Fije , el número de aristas en el grafo es :
n=4,5,6,7
212,805,2910,10199
In[]:=
ResourceFunction["OEISLookup"][{212,805,2910,10199}]
Out[]=
A224327OEISLookup
La solución en forma cerrada es
Desde el punto de vista de la combinatoria, la fórmula en forma cerrada está respaldada por el siguiente argumento:
Matriz de adyacencia
Matriz de adyacencia
Visualice la matriz de adyacencia del grafo
CITE ESTE CUADERNO
CITE ESTE CUADERNO
Explicación visual del problema Putnam 2025 A3
por Shenghui Yang
Comunidad Wolfram, STAFF PICKS, 28 de diciembre de 2025
https://community.wolfram.com/groups/-/m/t/3598035
por Shenghui Yang
Comunidad Wolfram, STAFF PICKS, 28 de diciembre de 2025
https://community.wolfram.com/groups/-/m/t/3598035