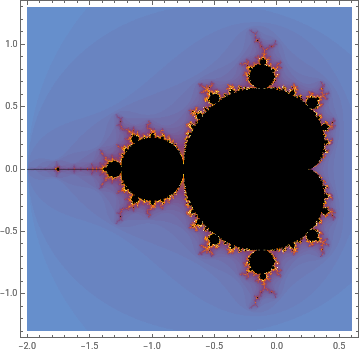
Dos perspectivas de z ↦ z² + c: El conjunto fractal de Mandelbrot muestra la conectividad del conjunto fractal de Julia asociado
Dos perspectivas de z ↦ z² + c: El conjunto fractal de Mandelbrot muestra la conectividad del conjunto fractal de Julia asociado
por Vitaliy Kaurov
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “Two views of z ↦ z² + c: Mandelbrot set fractal charts connectivity of related Julia set fractal” producido con ayuda de un LLM y verificado por un traductor profesional
Para video de alta calidad y discusión, vea:
El fractal de 𝓜𝐚𝐧𝐝𝐞𝐥𝐛𝐫𝐨𝐭 codifica los fractales de 𝓙𝐮𝐥𝐢𝐚.
Animación clave desarrollada: el 𝐩𝐮𝐧𝐭𝐨 𝐛𝐥𝐚𝐧𝐜𝐨 en 𝓜 define la conectividad de 𝓙.
A pesar de la definición de pocos símbolos 𝐙 ↦ 𝐙²+𝐂, ningún cálculo finito agota un fractal infinito. Cualquier algoritmo da solo aproximaciones. Al enfrentarse a universos infinitamente complejos e infinitamente explorables, el poder de la abstracción matemática es codificar lo infinito en forma simbólica finita. Algunos datos curiosos:
Animación clave desarrollada: el 𝐩𝐮𝐧𝐭𝐨 𝐛𝐥𝐚𝐧𝐜𝐨 en 𝓜 define la conectividad de 𝓙.
A pesar de la definición de pocos símbolos 𝐙 ↦ 𝐙²+𝐂, ningún cálculo finito agota un fractal infinito. Cualquier algoritmo da solo aproximaciones. Al enfrentarse a universos infinitamente complejos e infinitamente explorables, el poder de la abstracción matemática es codificar lo infinito en forma simbólica finita. Algunos datos curiosos:
Tanto los fractales de 𝓜𝐚𝐧𝐝𝐞𝐥𝐛𝐫𝐨𝐭 como de 𝓙𝐮𝐥𝐢𝐚 se definen como 𝐙 ↦ 𝐙²+ 𝐂
¿La diferencia? 𝓜 representa 𝐂, y 𝓙 representa 𝐙.
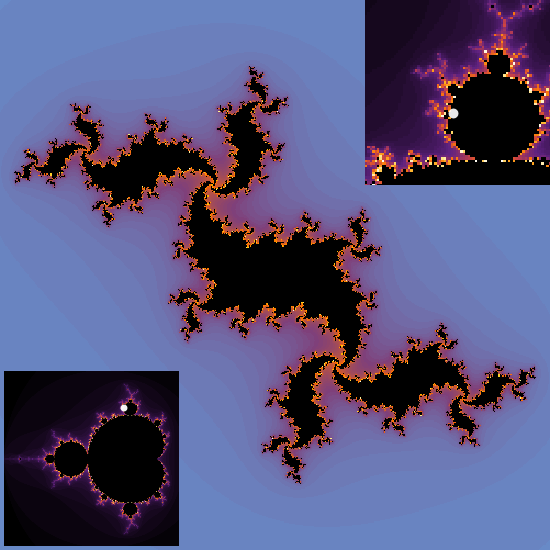
El punto blanco (parámetro 𝐂) se desplaza en el conjunto 𝓜 (esquinas) y el conjunto 𝓙 correspondiente se representa en el centro.
¿La diferencia? 𝓜 representa 𝐂, y 𝓙 representa 𝐙.
El punto blanco (parámetro 𝐂) se desplaza en el conjunto 𝓜 (esquinas) y el conjunto 𝓙 correspondiente se representa en el centro.
Por lo tanto: 𝓜𝐚𝐧𝐝𝐞𝐥𝐛𝐫𝐨𝐭 es un atlas para 𝓙𝐮𝐥𝐢𝐚.
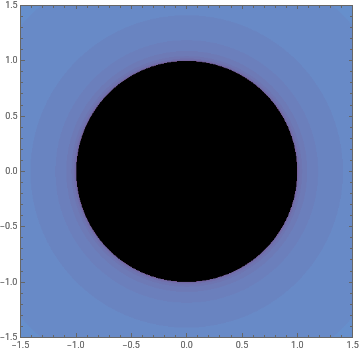
Significa que cada punto 𝐂 (punto blanco) en el conjunto 𝓜 indica la estructura del conjunto 𝓙 correspondiente. Si el punto blanco está dentro de 𝓜, entonces 𝓙(𝐂) es un todo conexo. Si el punto blanco está fuera de 𝓜, entonces 𝓙(𝐂) se fragmenta en polvo. El conjunto de Mandelbrot funciona como un mapa: al explorar el espacio de parámetros 𝐂, podemos clasificar cada conjunto de Julia posible según su conectividad.
En Wolfram Language, el código más simple puede representar estos fractales. Por ejemplo, las funciones a continuación ayudaron a crear este video. Representar Mandelbrot:
In[]:=
MandelbrotSetPlot[]
Out[]=
o incluso crear aplicaciones interactivas para Julia:
In[]:=
Manipulate[JuliaSetPlot[Complex@@p,PlotRange->1.5],{p,Locator},SaveDefinitions->True]
Out[]=
Asignemos un valor de 550 al parámetro de tamaño de imagen en las representaciones o visualizaciones posteriores:
In[]:=
grSZ=550;
Se define una lista de 13 puntos bidimensionales. Estos generan imágenes bonitas de Julia.
In[]:=
pts={{-0.205,0.686},{-0.297,0.648},{-0.216,0.707},{-0.2,0.806},{-0.117,0.862},{-0.203,0.811},{-0.218,0.712},{-0.285,0.638},{-0.186,0.653},{-0.086,0.658},{-0.087,0.668},{-0.187,0.673},{-0.187,0.663}};
Se crea una función B-spline utilizando este conjunto de puntos. Esta función representa una curva suave que interpola los puntos dados.
Está definida como cerrada, lo que significa que los puntos inicial y final de la curva son conexos.
Está definida como cerrada, lo que significa que los puntos inicial y final de la curva son conexos.
In[]:=
bsp=BSplineFunction@@ResourceFunction["CubicSplineCurve"][pts,SplineClosed->True]
Out[]=
BSplineFunction
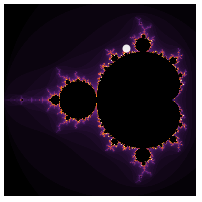
Se define una función para representar el conjunto de Mandelbrot, el cual es un fractal utilizado en la dinámica compleja. La representación gráfica incluye un pequeño disco blanco en una posición especificada, posiblemente para resaltar un punto de interés. Esto servirá más adelante como un recuadro adicional (inset).
In[]:=
mand[p_]:=MandelbrotSetPlot[ColorFunction->"SunsetColors",Frame->False,ImageSize->grSZ/3.,Epilog->{White,Disk[p,.01]},PlotRange->{{-.4,0},{.6,1}},PerformanceGoal->"Quality"]mand[{-.35,.7}]
Out[]=
In[]:=
mand2[p_]:=MandelbrotSetPlot[ColorFunction->"SunsetColors",Frame->False,ImageSize->grSZ/3.,Epilog->{White,Disk[p,.05]},PerformanceGoal->"Quality"]mand2[{-.35,.7}]
Out[]=
Se utiliza una función para crear una representación gráfica interactiva del conjunto de Julia, el cual es otro tipo de fractal relacionado con los números complejos. Incluye recuadros de las representaciones del conjunto de Mandelbrot creadas anteriormente, con los puntos resaltados calculados dinámicamente según la función B-spline. La visualización permite al usuario explorar diferentes conjuntos de Julia ajustando un parámetro.
In[]:=
Manipulate[JuliaSetPlot[Complex@@bsp[t],ImageSize->grSZ{1,1},PerformanceGoal->"Quality",PlotRange->1.4,Frame->False,Epilog->{Inset[mand[bsp[t]],{Right,Top},{Right,Top}],Inset[mand2[bsp[t]],{Left,Bottom},{Left,Bottom}]}],{t,0,1},SaveDefinitions->True]
Out[]=
CITE ESTE CUADERNO
CITE ESTE CUADERNO
Dos perspectivas de z ↦ z² + c: El conjunto fractal de Mandelbrot muestra la conectividad del conjunto fractal de Julia asociado
por Vitaliy Kaurov
Comunidad Wolfram, STAFF PICKS, 11 de septiembre de 2025
https://community.wolfram.com/groups/-/m/t/3543860
por Vitaliy Kaurov
Comunidad Wolfram, STAFF PICKS, 11 de septiembre de 2025
https://community.wolfram.com/groups/-/m/t/3543860