El caso continuo de la secuencia Q de Hofstadter
El caso continuo de la secuencia Q de Hofstadter
por Ed Pegg
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “The continuous case of the Hofstadter's Q-Sequence” producido con ayuda de un LLM y verificado por un traductor profesional
La función Q continua
La función Q continua
Hace un año, Stephen Wolfram escribió sobre Funciones recursivas anidadas. Le sugiero que reflexione sobre su columna.
In[]:=
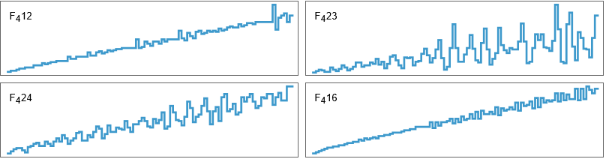
Grid[Partition[Function[{a,b},ListStepPlot[ResourceFunction["RecursiveFunction"][f[n]->f[n-f[n-a]]+f[n-f[n-b]],{n<=0->1}][Range[100]],Center,AspectRatio->1/4,ImageSize->300,Frame->True,FrameTicks->None,Epilog->Text[Row[{,a,b}],Scaled[{.03,.8}],{-1,0}]]]@@@{{1,2},{2,3},{2,4},{1,6}},2]]
"F"
4
Out[]=
Él está explorando cientos de funciones diferentes, así que ideó un código para ellas. La que llama 12 es la secuencia Q de Hofstadter.
F
4
In[]:=
g[n_?NumericQ]:=g[n]=If[n<3,1,g[n-g[n-1]]+g[n-g[n-2]]];
In[]:=
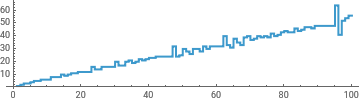
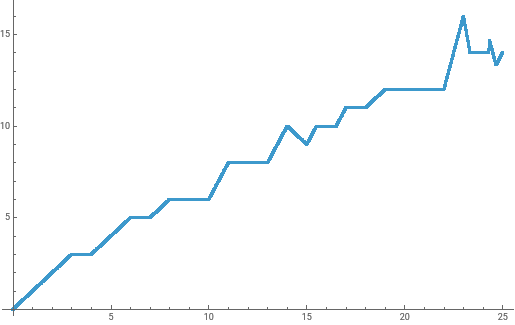
ListStepPlot[Table[g[n],{n,2,100}],Joined->True,AspectRatio->1/4]
Out[]=
In[]:=
Table[g[n],{n,2,55}]
Out[]=
{1,2,3,3,4,5,5,6,6,6,8,8,8,10,9,10,11,11,12,12,12,12,16,14,14,16,16,16,16,20,17,17,20,21,19,20,22,21,22,23,23,24,24,24,24,24,32,24,25,30,28,26,30,30}
Me preguntaba qué ocurriría si lo analizaba como una función continua. Resulta que se ve igual que la función entera.
In[]:=
Row[ListStepPlot[Table[{n,g[n]},{n,0,55,#}],ImageSize->300]&/@{1,1/50}]
Out[]=
Entonces, en lugar de g[2]=1, probé g[2]=2 en su lugar con una nueva función.
In[]:=
f[n_?NumericQ]:=f[n]=If[n<3,n,f[n-f[n-1]]+f[n-f[n-2]]];
Los resultados parecen similares, con un desfase de 1.
In[]:=
Table[f[n],{n,1,54}]
Out[]=
{1,2,3,3,4,5,5,6,6,6,8,8,8,10,9,10,11,11,12,12,12,12,16,14,14,16,16,16,16,20,17,17,20,21,19,20,22,21,22,23,23,24,24,24,24,24,32,24,25,30,28,26,30,30}
Para los primeros 50 000 enteros, .
f[n]=g[n+1]
In[]:=
Union[Table[f[n],{n,1,50000}]-Table[g[n],{n,2,50001}]]
Out[]=
{0}
La función tiene continuidad y mucha más complejidad. Denomino a esta variación la función Q continua.
In[]:=
ListPlot[Table[{n,f[n]},{n,0,55,1/120}]]
Out[]=
Parece sencillo hasta 25.
In[]:=
ListPlot[Table[{n,f[n]},{n,0,25,1/120}]]
Out[]=
Podemos obtener la función a trozos.
In[]:=
ClearAll[f,n];f[n_?NumericQ]:=f[n]=If[n<3,n,f[n-f[n-1]]+f[n-f[n-2]]];h=1/120;(*detectintegerslopeflipsupto20*)leftD[k_]:=(f[k]-f[k-h])/h;rightD[k_]:=(f[k+h]-f[k])/h;changeInts=Select[Range[3,20],Round[leftD[#]]=!=Round[rightD[#]]&];x=Rationalize[Range[3,25,h],0];y=f/@x;sl=Rationalize[Differences[y]/h,0];xL=Most[x];xR=Rest[x];idxRuns=SplitBy[Range[Length[sl]],sl[[#]]&];toPiece[idx_List]:=Module[{a=xL[[First[idx]]],b=xR[[Last[idx]]],m=sl[[First[idx]]],v0=f[xL[[First[idx]]]],c},c=v0-ma;(*y=mn+c*){mn+c,a<=n<b}];piecesGE3=toPiece/@idxRuns;pw=Piecewise[Prepend[piecesGE3,{n,n<3}],Indeterminate];
In[]:=
pw
Out[]=
|
Se complica más después de eso:
Se vuelve mucho, mucho peor después de 49.
El siguiente es código para extender la función a trozos por uno, y mostrar el estado a medida que la función a trozos crece:
Código para pw54
Código para pw54
pw54
pw54
He tenido que ejecutar esto varias veces porque 56 no se resuelve en mi sistema.
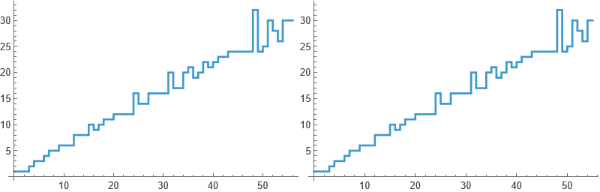
Si he calculado esto correctamente, esta es la tasa de crecimiento:
Nunca logré obtener 56. La última sección es más del doble de grande que todo lo demás combinado.
Doy las funciones a trozos tanto para 54 como para 55 porque mi computadora antigua no puede derivar 55 para la función a trozos.
Doy las funciones a trozos tanto para 54 como para 55 porque mi computadora antigua no puede derivar 55 para la función a trozos.
Por eso, simplifiqué pw55 a puntos.
La primera parte complicada:
La segunda parte, solo hasta el 54.
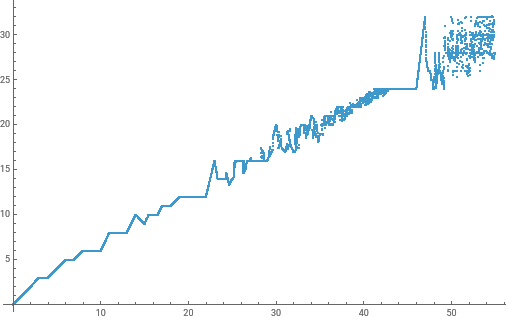
La función continua adquiere un nivel asombroso de complejidad en el intervalo de 52 a 55. Cada punto rojo es un punto de inflexión.
El denominador más grande en el rango llega hasta 1713454620:
¿Y ahora qué? La función es continua hasta 55, pero no estoy seguro de qué sucede en el intervalo de 55 a 95.
No estoy seguro de cómo obtener la función definida por tramos o una representación puntual hasta 56, o para valores mayores.
¿Cuál es la tasa de crecimiento para el número de tramos?
¿Otras funciones de las NFunciones recursivas anidadas se vuelven drásticamente más complejas en el caso continuo? ¿Cuáles son los monstruos?
No estoy seguro de cómo obtener la función definida por tramos o una representación puntual hasta 56, o para valores mayores.
¿Cuál es la tasa de crecimiento para el número de tramos?
¿Otras funciones de las NFunciones recursivas anidadas se vuelven drásticamente más complejas en el caso continuo? ¿Cuáles son los monstruos?
A veces, los problemas no resueltos pueden resolverse haciéndolos más complicados.
¿La función continua ayuda con la secuencia Q de Hofstadter?
¿La función continua ayuda con la secuencia Q de Hofstadter?
Me pregunto cuán complejo se vuelve esto para valores más altos.
CITE ESTE CUADERNO
CITE ESTE CUADERNO
El caso continuo de la secuencia Q de Hofstadter
por Ed Pegg
Comunidad Wolfram, STAFF PICKS, 24 de septiembre de 2025
https://community.wolfram.com/groups/-/m/t/3550911
por Ed Pegg
Comunidad Wolfram, STAFF PICKS, 24 de septiembre de 2025
https://community.wolfram.com/groups/-/m/t/3550911