La cuña de Mekhontsev: Una repitesela 3D
La cuña de Mekhontsev: Una repitesela 3D
por Ed Pegg
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “ The Mekhontsev wedge: A 3D rep-tile” producido con ayuda de un LLM y verificado por un traductor profesional
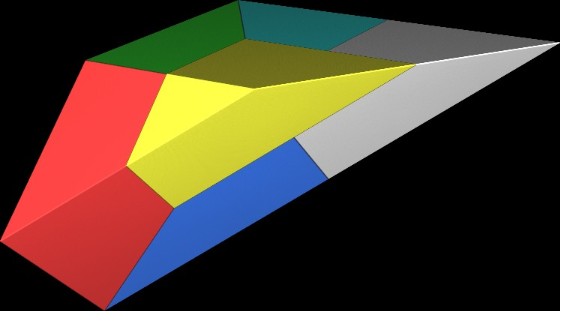
«Un poliedro convexo autosemejante no trivial (rep-8-tile, V=6 F=5 E=9) que encontré usando IFStile.» - Dmitry Mekhontsev
Aquí tenemos cómo hacerlo en WL:
In[]:=
wedge=ConvexHullMesh[{{0,0,0},{4,0,0},{4,4,0},{2,2,2},{4,2,2},{4,4,2}}];hull1=ConvexHullMesh[{{0,0,0},{2,0,0},{2,2,0},{1,1,1},{2,1,1},{2,2,1}}];hull2=ConvexHullMesh[{{1,1,1},{3,1,1},{3,3,1},{2,2,2},{3,2,2},{3,3,2}}];hull3=ConvexHullMesh[{{4,4,0},{4,2,0},{2,2,0},{3,3,1},{3,2,1},{2,2,1}}];hull4=ConvexHullMesh[{{4,0,0},{2,0,0},{2,2,0},{3,1,1},{2,1,1},{2,2,1}}];hull5=ConvexHullMesh[{{4,0,0},{4,2,0},{2,2,0},{3,1,1},{3,2,1},{2,2,1}}];hull6=ConvexHullMesh[{{4,0,0},{4,2,0},{4,2,2},{3,1,1},{3,2,1},{3,2,2}}];hull7=ConvexHullMesh[{{4,4,0},{4,2,0},{4,2,2},{3,3,1},{3,2,1},{3,2,2}}];hull8=ConvexHullMesh[{{4,4,0},{4,4,2},{4,2,2},{3,3,1},{3,3,2},{3,2,2}}];Graphics3D[{Opacity[0.9],Black,Thick,MeshPrimitives[wedge,1],White,Opacity[0.4],MeshPrimitives[hull1,2],MeshPrimitives[hull2,2],MeshPrimitives[hull3,2],MeshPrimitives[hull4,2],MeshPrimitives[hull5,2],MeshPrimitives[hull6,2],MeshPrimitives[hull8,2]},Boxed->False]
Out[]=
Esta es una forma más compacta:
In[]:=
pts={{0,0,0},{2,0,0},{2,2,0},{1,1,1},{2,1,1},{2,2,1}};oct=FiniteGroupData["Octahedral","MatrixRepresentation"];xf={{1,{0,0,0}},{1,{1,1,1}},{8,{4,4,0}},{21,{4,0,0}},{16,{4,0,0}},{25,{4,0,0}},{44,{4,4,0}},{9,{4,4,0}}};hulls=pts.oct[[#[[1]]]]+Table[#[[2]],{6}]&/@xf;Graphics3D[{Opacity[0.9],MeshPrimitives[ConvexHullMesh[#],2]&/@hulls},Boxed->False]
Out[]=
O, de manera aún más compacta:
In[]:=
hulls=IntegerDigits[#,10,3]&/@#&/@{{000,200,220,111,211,221},{111,311,331,222,322,332},{440,420,220,331,321,221},{400,200,220,311,211,221},{400,420,220,311,321,221},{400,420,422,311,321,322},{440,420,422,331,321,322},{440,442,422,331,332,322}};Graphics3D[{Opacity[0.7],MeshPrimitives[ConvexHullMesh[#],2]&/@hulls},Boxed->False]
Out[]=
Repitamos el mapeo:
In[]:=
big={{0,0,0},{4,0,0},{4,4,0},{2,2,2}};bary=ResourceFunction["Areal"][big,#]&/@Flatten[hulls,1];wedges=Flatten[Table[Partition[ResourceFunction["Areal"][Take[hulls[[j]],4],#]&/@bary,6],{j,1,8}],1];Graphics3D[{Opacity[.4],MeshPrimitives[ConvexHullMesh[#],2]&/@wedges},Boxed->False,SphericalRegion->True]
Out[]=
Llevémoslo a otro nivel:
In[]:=
big={{0,0,0},{4,0,0},{4,4,0},{2,2,2}};bary=ResourceFunction["Areal"][big,#]&/@Flatten[hulls,1];wedges2=Flatten[Table[Partition[ResourceFunction["Areal"][Take[wedges[[j]],4],#]&/@bary,6],{j,1,64}],1];Graphics3D[{Opacity[.3],MeshPrimitives[ConvexHullMesh[#],2]&/@wedges2},Boxed->False,SphericalRegion->True]
Out[]=
CITE ESTE CUADERNO
CITE ESTE CUADERNO
La cuña de Mekhontsev: Una repitesela 3D
por Ed Pegg
Comunidad Wolfram, STAFF PICKS, 20 de enero de 2026
https://community.wolfram.com/groups/-/m/t/3615445
por Ed Pegg
Comunidad Wolfram, STAFF PICKS, 20 de enero de 2026
https://community.wolfram.com/groups/-/m/t/3615445