La curva Kochawave y otros fractales
La curva Kochawave y otros fractales
por Ed Pegg
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “The Kochawave curve and other fractals” producido con ayuda de un LLM y verificado por un traductor profesional.
Rémy Sigrist escribió el artículo “La curva Kochawave, una variante de la curva de Koch”, así que pensé en probarla.
KochwavePoints[n_Integer?NonNegative]:=Module[{ω=Exp[IPi/3],steps=4^n,z,uk,vk},z=ConstantArray[0,steps+1];Do[uk=DigitCount[k,4,1];vk=DigitCount[k,4,2];z[[k+2]]=z[[k+1]]+(1+ω)^uk/ω^(2vk),{k,0,steps-1}];Transpose[{Re[z/3^n],Im[z/3^n]}]];KochwaveCurve[n_Integer?NonNegative]:=Line[KochwavePoints[n]];
In[]:=
kp=KochwavePoints[6];Graphics[{EdgeForm[{Thin,Black}],Cyan,Polygon[Append[kp,{0,0}]]},PlotRange->All,AspectRatio->Automatic,ImageSize->800]
Out[]=
Un método más sencillo, pero algo sale mal con el último segmento:
In[]:=
Graphics@KochCurve2,{1,0},,30°,{1,-150°},{1,120°}
3
3
Out[]=
Un método para que KochCurve funcione correctamente:
In[]:=
Graphics@KochCurve5,{1,0},,30°,{1,-150°},{1,120°},{1/100000,0}
3
3
Out[]=
Benoit Mandelbrot nació el 20 de noviembre de 1924. Para su 101º cumpleaños, estaré dando una charla en línea gratuita sobre fractales a las 11 a. m., hora de Chicago. Hay miles de fractales escritos en Wolfram Language, así que destacaré cerca de un centenar de ellos.
In[]:=
ResourceFunction["SchmidtArrangements"][-3,"MinCurvature"->0,"MaxCurvature"->10,"Color"->{"ColorSaul",{2,1,1}},"Transparency"->"Increasing","Filter"->Rectangle[{-2.1,-Sqrt[3.0]-0.1},{2.1,2*Sqrt[3.0]+0.1}],PlotRange->{{-2,2},{0,Sqrt[3.0]}},ImageSize->Large]
Out[]=
Y el fractal Pinwheel:
In[]:=
ResourceFunction["AlgebraicSubstitutionTiling"]["Pinwheel",4,{"N","Start"->{{{0,0},{0,1},{2,1}},{{2,1},{2,0},{0,0}}}}]
Out[]=
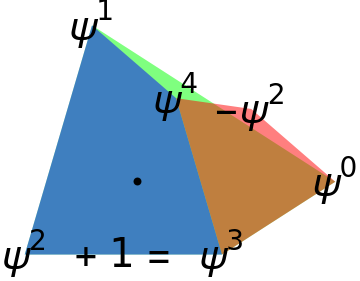
O el triángulo super áureo construido a partir del fractal PsiQuad. Si encuentra una solución compleja de +1=, entonces las potencias de ese valor dan los vértices de un sistema de sustitución. Es un fractal autogenerado.
2
ψ
3
ψ
In[]:=
{ψ,ψn,ψp}=x/.Solve[x^2+1==x^3‸];ψvals=ReIm/@{,,,,,-};ψtext={"","","","","","-"};pols={{1,2,3,4},{2,3,4,5},{5,4,1,6}};Graphics[{Opacity[.5],MapIndexed[{Hue[#2[[1]]/3],Polygon[ψvals[[#1]]]}&,pols],Opacity[1],Table[Style[Text[ψtext[[n]],ψvals[[n]]],40],{n,1,6}],Style[Text["+ 1 =",Mean[ψvals[[{3,4}]]]],40],Disk[{0,0},.02]}]
0
ψp
1
ψp
2
ψp
3
ψp
4
ψp
2
ψp
0
ψ
1
ψ
2
ψ
3
ψ
4
ψ
2
ψ
Out[]=
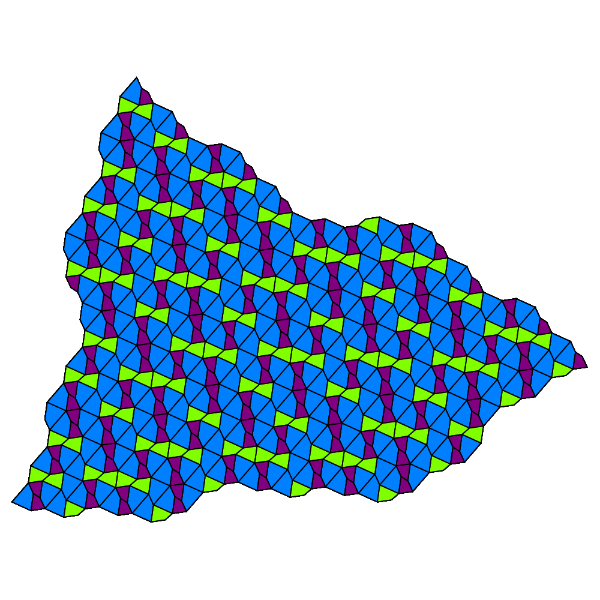
Esto conduce al triángulo fractal super áureo:
In[]:=
ResourceFunction["AlgebraicSubstitutionTiling"]["PsiQuad",16,{"N","ImageSize"{600,410}}]
Out[]=
La super razón áurea es una suma infinita de sus propias potencias recíprocas:
Lo cual lleva a la espiral de nautilus del triángulo super áureo:
Para estos y más, asista a mi charla gratuita en línea sobre fractales a las 11:00 a. m., hora de Chicago, el jueves 20 de noviembre.
CITE ESTE CUADERNO
CITE ESTE CUADERNO
La curva Kochawave y otros fractales
por Ed Pegg
Comunidad Wolfram, STAFF PICKS, 19 de noviembre de 2025
https://community.wolfram.com/groups/-/m/t/3577688
por Ed Pegg
Comunidad Wolfram, STAFF PICKS, 19 de noviembre de 2025
https://community.wolfram.com/groups/-/m/t/3577688