[このノートブックは以下のcommunityのポストをLLMツールにより日本語に翻訳したものです：
​The Continuous case of the Hofstadter’s Q-Sequence​
by Ed Pegg​
Wolfram Community, STAFF PICKS, September 24, 2025
​https://community.wolfram.com/groups/-/m/t/3550911]

HofstadterのQ数列の連続の場合

by Ed Pegg

連続Q関数

一年前，Stephen Wolframは入れ子状の再帰関数について執筆した． Wolframのコラムをぜひ熟考されたい．
In[]:=
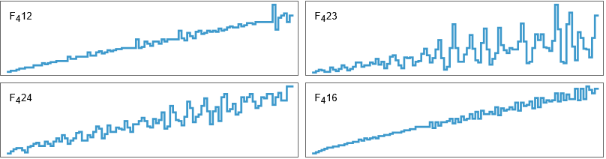
Grid[Partition[Function[{a,b},​​ListStepPlot[ResourceFunction["RecursiveFunction"][​​f[n]->f[n-f[n-a]]+f[n-f[n-b]],{n<=0->1}​​][Range[100]],Center,​​AspectRatio->1/4,ImageSize->300,Frame->True,FrameTicks->None,Epilog->Text[Row[{
"F"
4
,a,b}],Scaled[{.03,.8}],{-1,0}]]]@@@{{1,2},{2,3},{2,4},{1,6}},2]]
Out[]=
何百もの異なる関数を探求しているため，それらに対するコードを考案したのである．
F
1
12
と呼んでいるものは，HofstadterのQ数列である．
In[]:=
g[n_?NumericQ]:=g[n]=If[n<3,1,g[n-g[n-1]]+g[n-g[n-2]]];
In[]:=
ListStepPlot[Table[g[n],{n,2,100}],Joined->True,AspectRatio->1/4]
Out[]=
整数の場合は有名で複雑である．
In[]:=
Table[g[n],{n,2,55}]
Out[]=
{1,2,3,3,4,5,5,6,6,6,8,8,8,10,9,10,11,11,12,12,12,12,16,14,14,16,16,16,16,20,17,17,20,21,19,20,22,21,22,23,23,24,24,24,24,24,32,24,25,30,28,26,30,30}
これを連続関数として考察した場合，どのような挙動を示すかと疑問に思った．結果として，整数関数と同様の見た目となる．
In[]:=
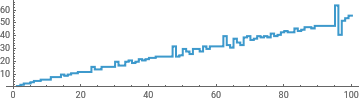
Row[ListStepPlot[Table[{n,g[n]},{n,0,55,#}],ImageSize->300]&/@{1,1/50}]
Out[]=
したがって，g[2]=1 の代わりに，新たな関数を用いて g[2]=2 として試行した．
In[]:=
f[n_?NumericQ]:=f[n]=If[n<3,n,f[n-f[n-1]]+f[n-f[n-2]]];
結果は類似しているが，1のオフセットが存在する．
In[]:=
Table[f[n],{n,1,54}]
Out[]=
{1,2,3,3,4,5,5,6,6,6,8,8,8,10,9,10,11,11,12,12,12,12,16,14,14,16,16,16,16,20,17,17,20,21,19,20,22,21,22,23,23,24,24,24,24,24,32,24,25,30,28,26,30,30}
最初の50000個の整数について，
f[n]=g[n+1]
となる．
In[]:=
Union[Table[f[n],{n,1,50000}]-Table[g[n],{n,2,50001}]]
Out[]=
{0}
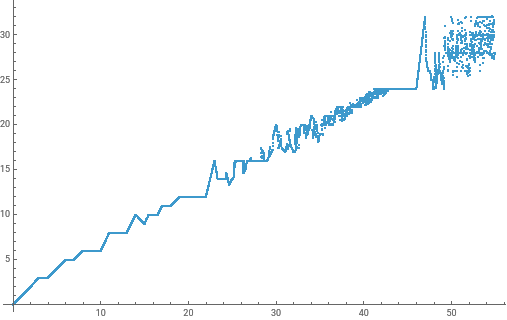
この関数は連続性を有し，さらに多くの複雑性を持つ．この変種を連続Q関数と名付ける．
In[]:=
ListPlot[Table[{n,f[n]},{n,0,55,1/120}]]
Out[]=
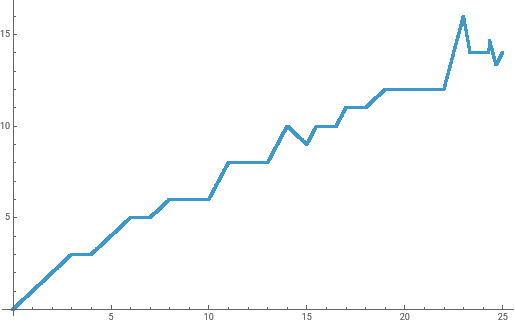
25までにおいては単純に見える．
In[]:=
ListPlot[Table[{n,f[n]},{n,0,25,1/120}]]
Out[]=
区分的関数を取得することが可能である．
In[]:=
ClearAll[f,n];​​f[n_?NumericQ]:=f[n]=If[n<3,n,f[n-f[n-1]]+f[n-f[n-2]]];​​h=1/120;​​(*detectintegerslopeflipsupto20*)​​leftD[k_]:=(f[k]-f[k-h])/h;​​rightD[k_]:=(f[k+h]-f[k])/h;​​changeInts=Select[Range[3,20],Round[leftD[#]]=!=Round[rightD[#]]&];​​x=Rationalize[Range[3,25,h],0];​​y=f/@x;​​sl=Rationalize[Differences[y]/h,0];​​xL=Most[x];xR=Rest[x];​​idxRuns=SplitBy[Range[Length[sl]],sl[[#]]&];​​toPiece[idx_List]:=Module[{a=xL[[First[idx]]],b=xR[[Last[idx]]],m=sl[[First[idx]]],v0=f[xL[[First[idx]]]],c},c=v0-ma;(*y=mn+c*){mn+c,a<=n<b}];​​piecesGE3=toPiece/@idxRuns;​​pw=Piecewise[Prepend[piecesGE3,{n,n<3}],Indeterminate];
In[]:=
pw
Out[]=
n
n<3
3
3≤n<4
-1+n
4≤n<6
5
6≤n<7
-2+n
7≤n<8
6
8≤n<10
-14+2n
10≤n<11
8
11≤n<13
-18+2n
13≤n<14
24-n
14≤n<15
-21+2n
15≤n<
31
2
10
31
2
≤n<
33
2
-23+2n
33
2
≤n<17
11
17≤n<18
-7+n
18≤n<19
12
19≤n<22
-76+4n
22≤n<23
154-6n
23≤n<
70
3
14
70
3
≤n<
1457
60
-
1373
6
+10n
1457
60
≤n<
583
24
-326+14n
583
24
≤n<
73
3
112-4n
73
3
≤n<
74
3
-36+2n
74
3
≤n<25
Indeterminate
True
その後はさらに複雑になる:
49を超えた後，状況はさらに著しく複雑になる:
以下に，区分的関数を1つ拡張し，区分的関数が増加する過程における状態を提供するためのコードを示す．

pw54のコード

pw54

著者のシステムにおいて56が解決されないため，これを数回実行する必要があった．
これらの計算が正しければ，成長率は次の通りとなる:
56を得ることは一度もできなかった．最後の区間は他の全てを合わせたものの2倍以上の大きさとなっている．
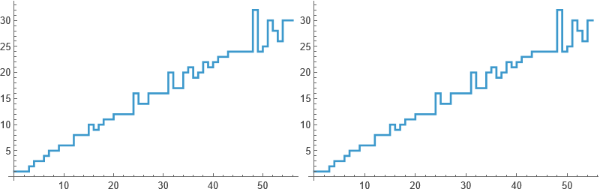
区分的関数については，古いコンピュータでは55を動作させることができないため，54および55の区分的関数を示す．
そのため，pw55を点に簡略化した．
最初の複雑な部分：
第2部は，54までである．
連続関数は，52から55の範囲において非常に複雑な様相を呈する．各赤い点は感染点である．
この範囲における最大の分母は1713454620に達する:
それでは，次に何をすべきであろうか．本関数は55まで連続であるが，55から95の範囲でどのような挙動となるかは不明である．
区分的関数や点の表現を56やそれ以上の値までどのように得るべきか判断できない．
区分数に対する増加率はどのようになるか．
他の関数，すなわちNestedly Recursive Functions は，連続の場合において劇的に複雑さが増すのであろうか．また，「モンスター」とは何か．
時として，未解決問題は，より複雑にすることで突破口が見出される場合がある．
連続関数はHofstadter’s Q-Sequenceに役立つのであろうか．
より高い値に対して，この複雑さがどの程度になるかについて考察する必要がある．

このノートブックを引用する

The Continuous case of the Hofstadter's Q-Sequence​
by Ed Pegg​
Wolfram Community, STAFF PICKS, September 24, 2025
​https://community.wolfram.com/groups/-/m/t/3550911