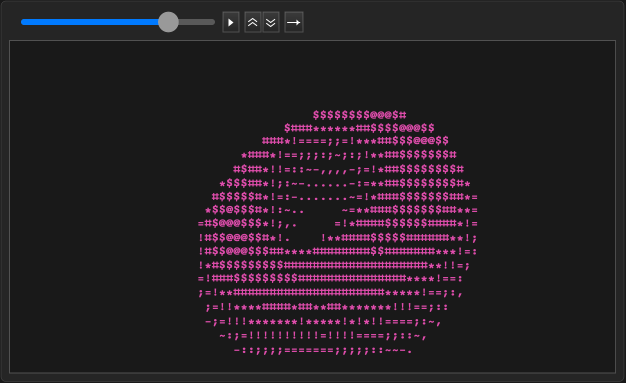
Reconstrucción de la clásica dona ASCII en Wolfram Language mediante FunctionCompile
Reconstrucción de la clásica dona ASCII en Wolfram Language mediante FunctionCompile
por Shenghui Yang
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “Reconstructing the classic ASCII donut in Wolfram language using FunctionCompile” producido con ayuda de un LLM y verificado por un traductor profesional
Este documento presenta una traducción de código de la donut.c de punto fijo de Andy Sloane a Wolfram Language, utilizando la característica FunctionCompile para un cálculo eficiente. El proyecto demuestra cómo los algoritmos C de nivel bajo pueden reproducirse fielmente en un entorno simbólico de alto nivel. Al combinar Style y ListAnimate, la implementación permite una animación fluida basada en ASCII con efectos de color personalizables.
In[]:=
Clear[RotateStep,IntDonutFrame];
Cree un entorno de compilador para almacenar las declaraciones de las funciones:
In[]:=
env=CreateCompilerEnvironment[];
CORDIC + paso de Newton para mantener la precisión en cálculos repetidos:
In[]:=
decl1=FunctionDeclaration[RotateStep,Typed[{"PackedArray"::["MachineInteger",1],"MachineInteger","MachineInteger"}->"PackedArray"::["MachineInteger",1]]@Function[{arg1,mul,shift},Module[{xx=arg1[[1]],yy=arg1[[2]],tmp,star},tmp=xx;xx=xx-BitShiftRight[mul*yy,shift];yy=yy+BitShiftRight[mul*tmp,shift];star=BitShiftRight[3145728-xx*xx-yy*yy,11];xx=BitShiftRight[xx*star,10];yy=BitShiftRight[yy*star,10];{xx,yy}]]];
Declare la función principal que maneja la rotación y la representación en ASCII:
In[]:=
decl2=FunctionDeclaration[IntDonutFrame,Typed[{"MachineInteger","MachineInteger","MachineInteger","MachineInteger"}->"ListVector"::["String"]]@Function[{cA,sA,cB,sB},Module[{w=80,h=22,chars={".",",","-","~",":",";","=","!","*","#","$","@"},b=CreateDataStructure["FixedArray"," ",1760],z=CreateDataStructure["FixedArray",127,1760],sj=0,cj=1024,si=0,ci=0,R1=1,R2=2048,K2=5120*1024,x0,x1,x2,x3,x4,x5,x6,x7,x,y,Nl=1,o=0,zz},Do[si=0;ci=1024;Do[x0=R1*cj+R2;x1=BitShiftRight[ci*x0,10];x2=BitShiftRight[cA*sj,10];x3=BitShiftRight[si*x0,10];x4=R1*x2-BitShiftRight[sA*x3,10];x5=BitShiftRight[sA*sj,10];x6=K2+R1*1024*x5+cA*x3;x7=BitShiftRight[cj*si,10];x=40+Quotient[30*(cB*x1-sB*x4),x6];y=12+Quotient[15*(cB*x4+sB*x1),x6];Nl=BitShiftRight[-cA*x7-cB*(BitShiftRight[-sA*x7,10]+x2)-ci*BitShiftRight[cj*sB,10],10];Nl=BitShiftRight[Nl-x5,7];o=x+80*y;zz=BitShiftRight[x6-K2,15];If[0<y<22&&0<x<80&&zz<z["Part",o+1],z["SetPart",o+1,zz];b["SetPart",o+1,chars[[If[Nl>0,Nl+1,1]]]]];{ci,si}=RotateStep[{ci,si},5,8];,{i,0,323,1}];{cj,sj}=RotateStep[{cj,sj},9,7];,{j,0,89,1}];b["Elements"]]]];
Coloque dos declaraciones en un solo entorno:
In[]:=
CompilerEnvironmentAppendTo[env,{decl1,decl2}]
Out[]=
CompilerEnvironmentObject
Compile la función de rotación y la función principal:
In[]:=
cfRotateStep=FunctionCompile[Function[{Typed[arg1,"PackedArray"::["MachineInteger",1]],Typed[m,"MachineInteger"],Typed[s,"MachineInteger"]},RotateStep[arg1,m,s]],CompilerEnvironment->env];
In[]:=
Information@cfRotateStep
Out[]=
In[]:=
cfIntDonutFrame=FunctionCompile[Function[{Typed[cA,"MachineInteger"],Typed[sA,"MachineInteger"],Typed[cB,"MachineInteger"],Typed[sB,"MachineInteger"]},IntDonutFrame[cA,sA,cB,sB]],CompilerEnvironment->env];
El resumen de la estructura interna de la función:
In[]:=
Information@cfIntDonutFrame
Out[]=
Use la función compilada cfRotateStep para crear una lista con 600 conjuntos de orientación para la dona 3D:
In[]:=
configs=Join@@@Transpose@{NestList[cfRotateStep[#,5,7]&,{0,1024},600],NestList[cfRotateStep[#,5,7]&,{1024,0},600]};
Distribuya las definiciones de mis funciones en subkernels:
In[]:=
Once[LaunchKernels[];DistributeDefinitions[cfRotateStep,cfIntDonutFrame]];
En mi Mac air M2, toma menos de dos segundos generar los 600 fotogramas en 8 subkernels paralelos:
In[]:=
AbsoluteTiming[data=ParallelMap[StringJoin/@Partition[cfIntDonutFrame[Sequence@@#],80]&,configs];]
Out[]=
{1.02595,Null}
Personalice el esquema de color usado en el ejemplo:
In[]:=
(*hbrw=RGBColor[107/256,218/256,70/256];tomatchcolorschemeinmactermimalhomebrewcolor*)clb=Blend[{White,RGBColor["#9B2A7F"],RGBColor["#748358"],RGBColor["#57C78B"],RGBColor["#E647AE"],White},#]&;
Ejecute la animación con otras opciones en la función Style para ajustar el tamaño. Se recomienda ejecutar el código en modo oscuro:
In[]:=
ListAnimate[Table[Style[Column[data[[i]],Spacings->0.2],Bold,FontFamily->"Courier",FontSize->12,clb[i/600](*hbrw*)],{i,600}],60,SaveDefinitions->True]
Out[]=
Esta versión compilada es aproximadamente 100 veces más rápida que la versión no compilada.
CITE ESTE CUADERNO
CITE ESTE CUADERNO
Reconstrucción de la clásica dona ASCII en Wolfram Language mediante FunctionCompile
por Shenghui Yang
Wolfram Community, STAFF PICKS, 24 de octubre de 2025
https://community.wolfram.com/groups/-/m/t/3564927
por Shenghui Yang
Wolfram Community, STAFF PICKS, 24 de octubre de 2025
https://community.wolfram.com/groups/-/m/t/3564927