Árboles de expansión mínimos aleatorios y la función zeta de Riemann

por Shenghui Yang
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “Random minimum spanning trees and Riemann Zeta function” producido con ayuda de un LLM y verificado por un traductor profesional
Considere el siguiente experimento:
1. Comience con un grafo completo de n nodos—cada nodo está conectado con todos los demás nodos.
2. Asigne a cada arista un peso aleatorio, elegido uniformemente del intervalo [0,1].
3. Calcule el árbol de expansión mínimo (MST) del grafo.
4. Registre la suma de los pesos de las aristas en ese MST.
Ahora repita este proceso a medida que
n
crece más y más. El hecho notable es el siguiente: el peso total esperado del MST aleatorio se aproxima al valor de la función zeta de Riemann en 3:
In[]:=
Style
apery’s constant
MATHWORLD TERMS

definition
[[1]],12,FontFamily->"Arial"//Framed
Out[]=
Apéry’s constant is defined by
ζ(3)1.2020569…,
(OEIS A002117) where
ζ(z)
is the Riemann zeta function. Apéry proved that
ζ(3)
is irrational, although it is not known if it is transcendental. Sorokin and Nesterenko subsequently constructed independent proofs for the irrationality of
ζ(3)
. Apéry’s proof involved use of the continued fraction
6
ζ(3)
5+
∞
K
n1
-
6
n
17
3
n
+
3
(n+1)
-12(2n+1)
.
En otras palabras, un proceso puramente combinatorio-probabilístico sobre grafos aleatorios le conduce de manera inesperada y directa a la famosa constante de Apéry. Este teorema fue demostrado rigurosamente por A.M. Frieze basado en el trabajo de Walkup, P. Erdös y A. Rényi.
Para fines de visualización, elija un grafo completo pequeño de manera que las etiquetas no estén demasiado agrupadas:
In[]:=
n=7;
Asigne uniformemente el peso entre [0,1] en cada arista:
In[]:=
ew=RandomReal[{0,1},Binomial[n,2]];
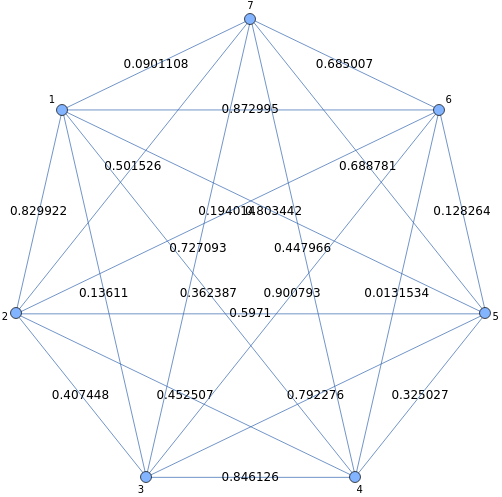
Visualice el grafo con el peso de las aristas:
In[]:=
g1=CompleteGraph[n,EdgeWeight->ew,EdgeLabels->"EdgeWeight",EdgeLabelStyle->12,VertexLabels->"Name"]
Out[]=
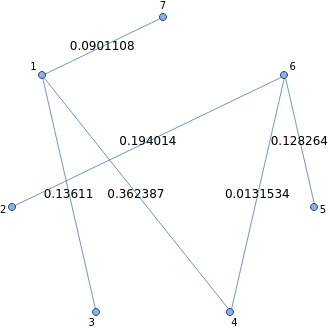
Encuentre el árbol de expansión mínimo como un subgrafo con pesos en las aristas:
In[]:=
mst=FindSpanningTree[g1,VertexLabels->"Name"];​​Grid[{mst,HighlightGraph[Annotate[g1,EdgeLabels->None],Style[mst,Thickness[0.03],StandardOrange]]}‸,Dividers->All]
Out[]=
Calcule la longitud del árbol de expansión mínimo
In[]:=
AnnotationValue[mst,EdgeWeight]
Out[]=
{0.13611,0.362387,0.0901108,0.194014,0.0131534,0.128264}
In[]:=
Total[%]
Out[]=
0.924039
Haga lo mismo para los grafos K-completos para
K=3,4,5,6,7,10,100,500
:
v={3,4,5,6,7,10,100,500};
In[]:=
res=Mean@Table[Total[AnnotationValue[​​FindSpanningTree@CompleteGraph[i,EdgeWeight->RandomReal[{0,1},Binomial[i,2]]]​​,EdgeWeight]],t,10‸,i,v‸]
Out[]=
{0.642456,0.860396,0.80748,1.08323,1.0249,1.00683,1.19652,1.21045,1.20355}
In[]:=
Grid[{v,res},Dividers->All]
Out[]=
3
4
5
6
7
10
100
500
1000
0.642456
0.860396
0.80748
1.08323
1.0249
1.00683
1.19652
1.21045
1.20355
También podemos probar el teorema repetidamente para un grafo completo de gran tamaño usando kernels paralelos:
In[]:=
LaunchKernels[];
Prueba sobre 1000 copias de 1000 grafos completos con pesos de arista aleatorios:
In[]:=
nv=1000;​​data=ParallelTable[Total[AnnotationValue[​​FindSpanningTree@CompleteGraph[nv,EdgeWeight->RandomReal[{0,1},Binomial[nv,2]]]​​,EdgeWeight]],{i,1000}];
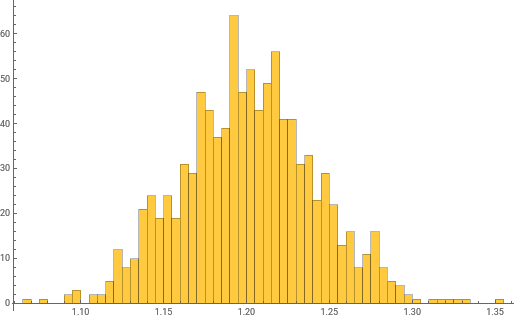
La distribución de las longitudes de sus árboles de expansión mínimos:
In[]:=
Histogram[data,{0.005}]
Out[]=
El valor es cercano a ζ(3):
In[]:=
{Mean[data],Zeta[3.]}
Out[]=
{1.20125,1.20206}

Referencia

A.M. Frieze, On the value of a random minimum spanning tree problem, Discrete Applied Mathematics, Volume 10, Issue 1, 1985,Pages 47-56, ISSN 0166-218X, https://doi.org/10.1016/0166-218X(85)90058-7.

CITE ESTE CUADERNO

Árboles de expansión mínimos aleatorios y la función zeta de Riemann​
por Shenghui Yang​
Comunidad Wolfram, STAFF PICKS, 17 de noviembre de 2025
​https://community.wolfram.com/groups/-/m/t/3577126