Mosaico con autómatas celulares coexistentes

por Phileas Dazeley-Gaist
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “Patchwork with coexisting cellular automata” producido con ayuda de un LLM y verificado por un traductor profesional

Introducción

En la Escuela de Verano Wolfram 2025, mientras asesoraba en un proyecto sobre la toma de decisiones colaborativa utilizando autómatas celulares (AC), dediqué algo de tiempo a idear diferentes configuraciones posibles para que las reglas de los AC interactuaran entre sí y realizaran “negociaciones”. Consideramos varias configuraciones, incluyendo el uso de las celdas de estado de AC para representar una distribución de opiniones en una sociedad, y probamos diversos esquemas en un intento de evolucionar reglas que produjeran de manera confiable estados de “consenso”.
Un enfoque que no tuve tiempo de explorar en profundidad, pero que mostró potencial, fue representar a los agentes como reglas confinadas a regiones específicas y estrictamente diferentes en el espacio, pero capaces de interactuar entre sí donde sus límites se tocan o están próximos. Configuraciones como esta serán el tema de este breve ensayo.
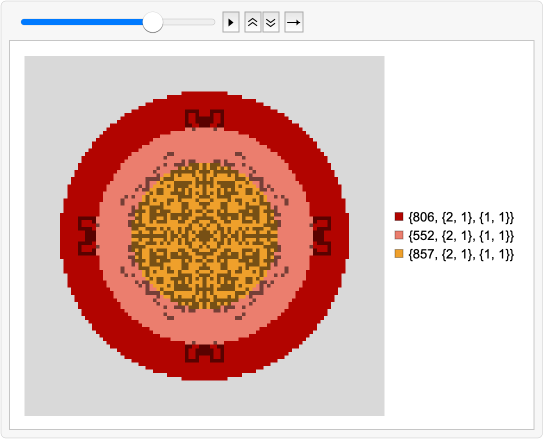
Este es un adelanto de lo que estamos desarrollando: programas que operan sobre arreglos de estados de autómatas celulares aplicando una lista de reglas de autómata celular a una lista de regiones no superpuestas del estado, de modo que cada región definida está sujeta a su propia dinámica, determinada tanto por la regla asignada a la región como por la dinámica cerca del límite de la región.
In[]:=
With[​​(*Defineparams:*)​​{simDuration=100,​​rules=({#1,{2,1},{1,1}}&)/@{806,552,857},​​init=SparseArray[ConstantArray[0,{101,101}]],​​domainMasks=ArrayPad[DiskMatrix[20],30]+ArrayPad[DiskMatrix[30],20]+ArrayPad[DiskMatrix[40],10],​​cf=ColorData[10]},​​​​(*Preparethebackgroundandlegend:*)​​{background=Colorize[domainMasks,ColorRules->Prepend[Thread[#->cf/@#]&@Range[Length[rules]],0->LightGray](*ColorFunction->(cf[1+Length[rules]*#]&)*)],​​legend=SwatchLegend[cf/@Range[Length[rules]],rules]},​​​​(*Computetrajectory:*)​​traj=CoexistingCellularAutomata[​​ (*Listofrules:*)rules,​​ (*Domainmasks:*)domainMasks,​​ (*Initialstate:*)init,​​ (*Numberofsteps:*)simDuration,​​ "GlobalMaskFunction"->(ArrayPad[DiskMatrix[40],10]&),​​ "GlobalMaskValueFunction"->(0&)​​],​​​​(*Animatetrajectoryframes:*)​​ListAnimate[Map[​​Labeled[Image[​​ImageCompose[​​background,​​{RemoveBackground[Image[1-#],White],.5}],​​ImageSize->Medium],​​legend,Right]&,traj]]​​]
Out[]=

Autómatas celulares con condiciones de frontera personalizadas

Avanzaremos gradualmente hasta llegar a los AC operando en paralelo sobre regiones del espacio que no se superponen. Pero primero, será útil repasar algunos de los conceptos básicos.

Automátas celulares unidimensionales

Condiciones de contorno de AC compatibles de forma nativa

En Wolfram Language, los autómatas celulares tienen por defecto condiciones de contorno periódicas.
Trayectoria de un autómata celular elemental con condiciones de contorno periódicas:
In[]:=
ArrayPlot[CellularAutomaton[28,ArrayPad[{1},50],100],ImageSize->Small]
Out[]=
Observe la cascada de ondas que envuelve el espacio horizontal al salir por la derecha y, simultáneamente, entrar por la izquierda.
La alternativa compatible de forma nativa a las condiciones de contorno periódicas en la función CellularAutomaton es tener autómatas celulares (AC) ejecutándose en un lienzo infinito.
Trayectoria de un autómata celular elemental en un lienzo infinito:
In[]:=
ArrayPlot[CellularAutomaton[28,{{1},0},100],ImageSize->Small]
Out[]=
Aquí, la anchura del arreglo de estados no está fijada. En este caso, la cascada de ondas simplemente se propaga hacia afuera para siempre, sin interrupciones.
El sistema que estamos imaginando requiere que implementemos condiciones de frontera personalizadas, para las cuales, hasta donde sé, no existe soporte incorporado en este momento. ¿Entonces, cómo podemos lograrlo?

Confinamiento de autómatas celulares a regiones en el espacio

Para confinar una regla a una región espacial dentro de un estado de AC, el enfoque general más sencillo que se me ocurre es aplicar la regla al estado completo, pero descartar todos los cambios en el estado fuera de la región asignada a la regla utilizando una máscara de región. Por ejemplo:
Trayectoria de un autómata celular de la regla 30 confinado a una pequeña región del espacio de simulación:
With[{steps=100,rule=30,ruleRegionMask=ArrayPad[ConstantArray[1,21],40],init=ArrayPad[{1},50]},​​(*Makeaspacetimeplotofthetrajectory:*)​​ArrayPlot[NestList[​​(*ComputethenextCAstate:*)​​(*​​1.Multiplythenewstatebytheruleregionmask,​​2.multiplythenegativeoftheruleregionmaskbytheinitialstate,​​3.Sumtheresultingarrays:*)​​(CellularAutomaton[rule,#]*ruleRegionMask)+(#*(1-ruleRegionMask))&,init,steps]+Table[ruleRegionMask,steps+1],ColorRules->{0->White,1->StandardGreen,2->Black},ImageSize->Small]]
Out[]=
En la representación gráfica anterior, la región verde representa el dominio espacial de la regla del autómata.
Los cambios realizados en el estado por la regla solo tendrán efecto dentro de la región verde.
Proceder de esta manera significa que, aunque el autómata verde no puede realizar cambios en las celdas fuera de la región verde, las celdas de la región verde cercanas al borde aún "perciben" y se ven afectadas por el estado de las celdas al otro lado del borde. Si el vecindario de una celda de la región verde contiene celdas de diferentes regiones, esos estados de celda se utilizan para determinar el nuevo estado de la celda, tal como se haría normalmente. Esto permite que los límites de las regiones del autómata sean porosos de forma predeterminada.
La dinámica en la región verde se ve afectada por la dinámica local fuera de la región verde.
En el presente ejemplo, el fondo se mantiene constante y uniforme. Pero no hay razón para que tenga que ser así.
Si el fondo fuera heterogéneo y dinámico, nuestra configuración funcionaría igual de bien, aunque la dinámica en la región verde sería diferente, ya que la evolución del estado estaría sujeta a distintos tipos de interferencia por la actividad local del fondo. Volveremos a este punto más adelante.
Otra aclaración importante es que, aunque en las simulaciones anteriores la regla elegida está confinada a una región con un límite espacial constante, la simulación en sí sigue operando en un espacio periódico. Esta distinción es esencial porque significa que las celdas en la periferia de la matriz de estados siguen considerándose adyacentes a las celdas en sus lados opuestos. En el ejemplo anterior, los lados izquierdo y derecho de la matriz de estados siguen estando conectados. Si la región asignada a una regla se extendiera de un extremo al otro del estado, sería posible que las cascadas de eventos envolvieran todo el sistema.
Trayectoria de un autómata celular de la regla 30 confinado a una región que se enrolla alrededor de los límites periódicos del espacio de simulación:
With[​​{steps=100,rule=30,ruleRegionMask=1-ArrayPad[ConstantArray[1,20],40]},​​{init=ConstantArray[1,100]*ruleRegionMask},​​(*Makeaspacetimeplotofthetrajectory:*)​​ArrayPlot[NestList[​​(*ComputethenextCAstate:*)​​(CellularAutomaton[rule,#]*ruleRegionMask)+(#*(1-ruleRegionMask))&,init,steps]+Table[ruleRegionMask,steps+1],ColorRules->{0->White,1->StandardGreen,2->Black},ImageSize->Small]]

Eliminación de la periodicidad espacial

Para eliminar también las condiciones de contorno periódicas del propio espacio, mi sugerencia es un poco improvisada pero funcional: rellene cualquier estado inicial de AC con suficientes ceros en todas las direcciones para evitar la interacción periódica en los bordes del arreglo de estados, calcule el siguiente paso y recorte el arreglo resultante para recuperar las dimensiones originales. Repita según sea necesario. Rellenar por el rango de vecindad del autómata es sencillo y garantiza ser suficiente (el relleno mínimo requerido depende de la vecindad utilizada por los autómatas en la simulación, por lo que no lo trataré aquí).
Trayectoria de un autómata celular con un AC de regla 30 confinado a una región visualmente idéntica a la del ejemplo anterior, pero que no se envuelve alrededor de los límites periódicos del espacio de simulación:
Elegimos tener condiciones de frontera uniformes y constantes iguales a cero para todo el espacio de simulación, pero como antes, podríamos haberlo hecho de otra manera. Aquí hay un ejemplo en el que estas condiciones de frontera son aleatorias y dinámicas.
Trayectoria del autómata celular de regla 30 confinada a una región sujeta a condiciones de frontera aleatorias y dinámicas:
Aquí, los estados de las celdas que conforman el borde cambian al azar, afectando la dinámica del autómata verde, aunque el borde en sí no se desplaza. El borde está fijo en el espacio, pero no fijo en estado.

Automátas celulares bidimensionales

Ahora que hemos establecido algunas técnicas para confinar autómatas celulares unidimensionales a regiones específicas, el siguiente paso natural es aplicar estas ideas a los autómatas celulares bidimensionales. ¡Buenas noticias! Las técnicas que acabamos de discutir para los autómatas celulares unidimensionales funcionan igual de bien en dos dimensiones, e incluso en dimensiones superiores.
Aquí tenemos una configuración en dos dimensiones que confina un AC totalista de 9 vecinos a una región cuadrada del espacio de simulación.
Dinámica de un AC totalista de 9 vecinos confinado a una región cuadrada del espacio de simulación:
Igual que antes:
◼
  • La región verde representa el dominio espacial de la regla del autómata.
    • ◼
  • La frontera es porosa, por lo que la actividad cercana fuera de la región verde puede afectar la dinámica de la región verde.
    • ◼
  • Las condiciones de frontera para todo el espacio de simulación siguen siendo periódicas por defecto, pero pueden fijarse o controlarse utilizando las técnicas de enmascaramiento que describí para los AC unidimensionales.
    • Dado que la región verde está determinada por una matriz de máscara binaria, podemos probar fácilmente casi cualquier configuración que se le ocurra pintar sobre un lienzo. En los siguientes ejemplos, utilizo una región con una parte interna aislada con condiciones de frontera constantes iguales a cero, y una parte externa que conecta cada borde de la ventana de simulación. La parte interna permanecerá sin alteraciones ante cualquier cambio en las condiciones de frontera globales del espacio de simulación, por lo que su dinámica puede considerarse como un control en nuestros experimentos.
    Esta es una configuración donde la región verde permite que la dinámica se envuelva alrededor de cada eje.
    Dinámica de autómatas celulares totalísticos de 9 vecinos restringida a una región con un componente central aislado sujeto a condiciones de frontera fijas en cero, y un componente circundante sujeto a las condiciones de frontera periódicas del espacio de simulación:
    4
    /
    4
    Cellular automaton dynamics with an isolated central region and a surrounding region subject to periodic boundary conditions.
    Puede imaginar que el espacio se enrolla alrededor de un toro de la siguiente manera:
    Esta es una configuración con la misma especificación de la región verde, pero con condiciones de contorno constantes iguales a cero aplicadas al espacio de simulación.
    Dinámica de AC totalista de 9 vecinos restringida a una región con un componente central aislado sujeto a condiciones de contorno fijas en cero, y un componente circundante también sujeto a condiciones de contorno fijas:
    Establecer condiciones de frontera constantes en cero convierte los bordes de la ventana de simulación en paredes lisas, sólidas e impenetrables, impidiendo que la dinámica del AC verde se envuelva alrededor.
    Finalmente, aquí hay un ejemplo en el que estas condiciones de frontera se hacen aleatorias y dinámicas.
    Dinámica de autómatas celulares totalísticos de 9 vecinos restringida a una región con un componente central aislado sujeto a condiciones de contorno fijas en cero, y un componente circundante sujeto a condiciones de contorno dinámicas aleatorias:
    En este último caso, la dinámica en la parte exterior parece bastante aleatoria.

    Tres dimensiones y más

    Solo para demostrar que es posible, aquí hay un ejemplo complicado en 3D que utiliza un estado generado por otro AC 3D como la máscara de región del autómata:
    Dinámica de un AC tridimensional confinado a una región 3D compleja.
    Y aquí tenemos una simulación del proceso en seis dimensiones, solo por diversión, aunque ya no hay una forma sencilla de visualizar su salida, así que lo único que le mostraré es esta vista previa del arreglo de estado final:

    Bonus: Ejemplos interesantes diversos

    Laberintos

    Genere un laberinto para usar como máscara:
    Calcule la trayectoria de un autómata celular totalista bidimensional de 9 vecinos confinado por la máscara:

    Otras formas complejas

    Defina una forma orgánica para usar como una máscara:
    Calcule la trayectoria de un AC totalista 2D de 9 vecinos confinado por la máscara:

    Revisión

    En esta sección, exploramos técnicas para confinar autómatas celulares a regiones espaciales específicas dentro de un sistema de AC más grande. En resumen:
    ◼
  • Para confinar una regla de AC a una región espacial específica, podemos aplicar la regla al estado completo, pero descartar todos los cambios fuera de la región asignada de la regla utilizando una máscara de región.
    • ◼
  • Para eliminar las condiciones de contorno periódicas del propio espacio, podemos rellenar el estado inicial con suficientes ceros en todas las direcciones para evitar la interacción periódica en los bordes, calcular el siguiente paso y recortar el arreglo resultante para que vuelva a las dimensiones originales. Esto simula de manera efectiva condiciones de contorno constantes de valor cero.
    • ◼
  • También podemos hacer que las condiciones de frontera del espacio de simulación sean dinámicas y heterogéneas, por ejemplo, definiendo una máscara de frontera global que delimite la ventana de simulación y configurando las celdas dentro de la frontera que define en estados aleatorios en cada paso de la simulación. Cualquier CA cuyo dominio espacial esté lo suficientemente cerca de la máscara de frontera global verá sus dinámicas afectadas por las condiciones de frontera globales aleatorias.
    • ◼
  • Estas técnicas pueden aplicarse a autómatas celulares unidimensionales y bidimensionales, pero también a autómatas celulares en espacios de mayor dimensión.

    • Autómatas celulares coexistentes:
    Ejecución de AC en paralelo en regiones separadas del espacio

    ¿Cómo funciona?

    Podemos utilizar las herramientas desarrolladas anteriormente para realizar simulaciones en las que varias reglas de AC operan en paralelo sobre regiones no superpuestas del espacio de simulación. Me referiré a simulaciones como estas como AC coexistentes y, dado que querré experimentar mucho con los AC coexistentes, definiré una función CoexistingCellularAutomata para automatizar el proceso de configurar y ejecutar estas simulaciones.
    La definición completa de la función se puede encontrar en la sección Inicialización de código al final de este ensayo.
    Los pasos principales del proceso son:
    1
    .
    Defina una lista de reglas de AC y un estado inicial para todo el espacio de simulación.
    2
    .
    Cree un arreglo que especifique el dominio espacial para cada regla de AC, donde cada celda del arreglo corresponde al índice de la regla que debe aplicarse en esa región.
    3
    .
    Genere máscaras binarias a partir del arreglo de dominios espaciales para aislar las regiones donde debe aplicarse cada regla.
    4
    .
    Defina condiciones de frontera para el espacio total de simulación, las cuales pueden ser constantes o dinámicas.
    5
    .
    Aplique las reglas de AC a sus respectivos dominios, recorte los resultados usando las máscaras de dominio, sume los arreglos de estado resultantes y aplique las condiciones de frontera globales.

    Cálculo de un solo paso de una simulación de un AC coexistente

    Realización de una simulación completa de AC coexistentes

    La función CoexistingCellularAutomata facilita mucho configurar y realizar simulaciones de autómatas celulares que interactúan entre sí. Permítame mostrarle.
    Comenzaré definiendo mis parámetros de simulación. Para este ejemplo, elegiré 10 reglas al azar.
    A cada dominio de regla se le asignará su propio color.
    Elija algunas reglas totalísticas de AC de 2 colores y 9 vecinos al azar:
    Estableceré condiciones iniciales constantes de valor cero en todo el estado inicial.
    Los dominios espaciales de cada regla de AC en la simulación deben especificarse utilizando una sola matriz de valores enteros que correspondan a los índices de las reglas proporcionadas en la lista de reglas, o cero, lo que significa “no se aplica ninguna regla aquí”.
    Podemos dividir arbitrariamente el espacio de simulación y asignar las partes que elijamos a las reglas que deseemos. Aquí he utilizado una función auxiliar llamada generateVoronoiCASpatialDomains (definida en la sección Inicialización de código al final de este ensayo) para generar el arreglo de definiciones de dominios de reglas.
    Defina los dominios espaciales de cada regla en el espacio de simulación:
    Previsualice las máscaras de dominio:
    Para realizar una simulación, simplemente proporcione la lista de reglas, la máscara de dominio, el estado inicial y el número de pasos a la función CoexistingCellularAutomata.
    Realice una simulación usando CoexistingCellularAutomata:
    El resultado es una lista de arreglos que representan la secuencia de estados coexistentes de AC, cada uno de los cuales podemos representar para crear los fotogramas de una animación de toda la trayectoria de la simulación.
    Anime la simulación resultante de los AC interactuando, usando las máscaras para colorear los fotogramas:

    Uso de imágenes como máscaras de dominios coexistentes de AC

    La función CoexistingCellularAutomata funciona con definiciones arbitrarias válidas de dominio de reglas. Cualquier arreglo de valores enteros positivos o cero es una máscara de dominio de reglas válida. Esto significa que podemos usar imágenes posterizadas como especificaciones de dominios de reglas.
    Para este siguiente ejemplo, postericé un selfie de la webcam para que solo tuviera valores de píxel de 0, 1 o 2 y utilicé la imagen resultante como la especificación de máscara de dominio en CoexistingCellularAutomata.
    En la simulación, estos valores corresponden respectivamente a territorio neutral, el dominio de la primera regla y el dominio de la segunda regla. Elegí dos reglas totalistas de AC 2D con 9 vecinos para usar al azar:
    Defina una máscara para usar en la simulación:
    Configure y ejecute una simulación de 20 pasos con las reglas seleccionadas, los dominios de regla definidos por la máscara de imagen y una matriz de condición inicial compuesta completamente de ceros:

    Condiciones de contorno globales de las simulaciones de AC coexistentes

    Por defecto, CoexistingCellularAutomata asume condiciones de frontera periódicas en el espacio de simulación, como en esta trayectoria de la regla 10 y la regla 90, donde las celdas más a la izquierda del arreglo interactúan con las celdas más a la derecha:
    Como una comodidad para el usuario final, CoexistingCellularAutomata también permite especificar condiciones de frontera globales utilizando las opciones “GlobalMaskFunction” y “GlobalMaskValueFunction”. Como sugieren sus nombres, estas opciones están diseñadas para recibir argumentos de función. Estas deben ser funciones del arreglo de estados en un momento dado, aunque también se pueden definir para que ignoren la entrada del arreglo de estados.
    La opción “GlobalMaskFunction” define el límite de la simulación devolviendo una máscara binaria donde los 1 representan celdas que pueden ser afectadas por las reglas de AC elegidas y los 0 representan celdas que no pueden serlo. La función especificada también puede devolver un 0, lo que indica que no se deben añadir condiciones globales especiales de frontera. “GlobalMaskValueFunction” define los valores dentro de la región de frontera, y puede devolver un valor constante de estado de celda o un arreglo de estados válidos de celda.
    Cuando estas funciones devuelven arreglos, los mismos deben tener las mismas dimensiones que el arreglo de estados.
    Para añadir condiciones de contorno constantes de valor cero en los extremos izquierdo y derecho de los arreglos de estados en la simulación anterior, solo se necesitan cambios mínimos en el código. Al añadir
    and
    y
    a la llamada de función CoexistingCellularAutomata , restringimos los dominios de las reglas a todas las celdas excepto aquellas cercanas al borde, y establecemos que las celdas del borde excluidas sean iguales a 0 durante toda la simulación:
    Debido a que “GlobalMaskFunction” y “GlobalMaskValueFunction” esperan funciones, y estas funciones se calculan en cada paso de una simulación de AC coexistente, también es bastante sencillo establecer condiciones de frontera dinámicas. Si en cambio hubiéramos especificado las opciones
    y
    obtendríamos condiciones de contorno dinámicas aleatorias en los bordes del espacio de simulación:

    Reflexiones finales

    Hay muchas direcciones en las que este trabajo podría avanzar. Es fácil imaginar cómo las configuraciones que hemos explorado aquí podrían convertirse en la base de una especie de modelo de juguete de vida artificial, en el que los organismos sean autómatas celulares errantes cuyos límites espaciales estén sujetos a presiones ambientales y competitivas.
    Otra dirección podría ser modificar las configuraciones exploradas en este ensayo para permitir que múltiples AC ocupen los mismos dominios espaciales y compitan por la dominancia sobre estas regiones superpuestas. Esto requeriría una planificación cuidadosa, ya que existen muchas posibilidades sobre cómo podrían gestionarse dichas reclamaciones superpuestas, y todas inevitablemente tendrán sus propias ventajas y desventajas.
    ¿Qué haría usted a continuación? Si encuentra este trabajo interesante y desea comentarlo, no dude en ponerse en contacto. Soy bastante fácil de encontrar en línea, y estoy entusiasmado por seguir explorando este tema y ver qué puede surgir a partir de ello.

    Inicialización de código

    Implementación: CoexistingCellularAutomata

    Calcule trayectorias de múltiples AC coexistentes que ocupan regiones no superpuestas del espacio:

    Ejemplos con condiciones de contorno globales predeterminadas (espacio toroidal)

    Ejemplos con condiciones de contorno estáticas globales personalizadas

    Ejemplos con condiciones de contorno dinámicas globales personalizadas

    Implementación: ruleSpaceSize

    Obtenga el tamaño de un espacio de reglas de AC dado el número de estados en los que una celda puede estar y el tamaño del vecindario:

    Implementación: generateVoronoiCASpatialDomains

    Genere una partición espacial raster compuesta por n dominios contiguos utilizando una malla de Voronoi rasterizada:

    Ejemplos

    Un arreglo aleatorio de especificación de dominio espacial de AC coexistentes de Voronoi:
    Un arreglo de especificación de dominio espacial de AC coexistentes de Voronoi sembrado con puntos equidistantes en un círculo:
    Un arreglo de especificación de dominio espacial de AC coexistentes de Voronoi sembrado con puntos espaciados uniformemente a lo largo de una trayectoria espiral hexagonal:
    Un arreglo de especificación de dominio espacial de AC coexistentes de Voronoi sembrado con puntos equidistantes a lo largo de una trayectoria en espiral triangular:
    Un arreglo de especificación de dominio espacial de AC coexistentes de Voronoi sembrado con puntos equidistantes a lo largo de una trayectoria espiral cuadrada:

    CITE ESTE CUADERNO

    Patchwork with coexisting cellular automata​
    por Phileas Dazeley-Gaist​
    Comunidad Wolfram, STAFF PICKS, 17 de enero de 2026
    ​https://community.wolfram.com/groups/-/m/t/3608683