2025 年諾貝爾物理學獎：宏觀量子效應與量子電腦的曙光

by Mohammad Bahrami
熱烈祝賀 John Clarke、Michel H. Devoret 和 John M. Martinis 榮獲 2025 年諾貝爾物理學獎「在電路中發現了宏觀量子力學穿隧與能量量化現象。」他們的超導 Josephson 電路實驗，讓量子效應在電路尺度下無可爭議地展現出來，包括離散且非諧振的能階，以及在宏觀上可區分狀態之間的相干穿隧，為現代超導量子位元奠定了關鍵基礎。在這篇簡短的計算型文章中，我們將帶領大家通過簡明的模擬來重現這些特徵： 庫柏對盒/傳輸子的類能譜圖，以及帶有現實退相干的時域穿隧動力學，藉此呼應最初的實驗觀察結果。
​
​原創貼文

Josephson 電路（庫珀對盒／傳輸子範例）中的能量量子化

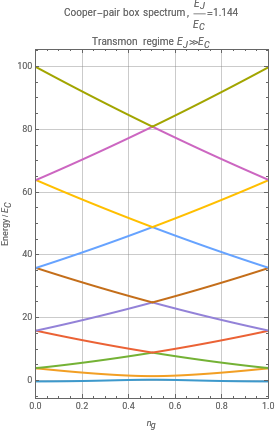
一個小型超導島，由 Josephson 接點和電容耦合方式至柵極，其變數以共軛變數描述：穿越接點的超導相位，以及島上庫珀對的整數數目。關鍵能量尺度包括由島電容決定的充電能、由接點的臨界電流決定的 Josephson 能，以及由柵極控制的偏置電荷。在電荷基底下，哈密頓變為一個實對稱三對角矩陣，主對角線上是充電項，最鄰近耦合則來自餘弦 Josephson 項； 對其進行對角化可得到離散、非諧性的能階。隨著 Josephson 能與充電能的比值增加，器件會由具有強烈偏置電荷離散性且在半整數偏置附近有明顯避免交叉的電荷量子位元區域，逐漸演化為具有抑制離散性且非諧性較弱、其非諧性由充電尺度決定的傳輸子區域。微波光譜學對柵極偏置（或相關裝置中的磁通）進行掃描，可以揭示這些離散躍遷及其非諧性， 而譜線寬則反映了其基礎相干時間。
考慮哈密頓，如

H
=4
2
E
C


n
-
n
g



-
E
J
cos

ϕ

，其中

n
為庫珀對的數目，具有整數本徵值，而 ϕ 為接面兩端的超導相位。 它們是正則共軛對：


ϕ
,

n
=
以及

n
=-
∂
∂ϕ
。此外
E
C
為充電能，
E
J
為 Josephson 能，
n
g
為閘極偏置電荷。此哈密頓可被視為一個在餘弦位勢中的量子轉子（相位），最小耦合到靜態的「向量勢」
n
g
，其使動量

n
發生位移。
電荷基底以
{|n〉}
nϵ
表示，其中

n
|n〉=n|n〉
。在此基底中，相位算符的作用如同階梯運算：
±

ϕ

|n〉=|n∓1〉
。因此， 這表示
cos

ϕ
=
1
2
∑
n
(|n〉〈n+1|+|n+1〉〈n|)
。將這些結合起來，哈密頓可在截斷的空間中描述，方法是設定
-
n
max
<=n<=
n
max
In[]:=
ClearAll[hamiltonian];​​hamiltonian[ratio_,ng_,nmax_:20]:=DiagonalMatrix[Table[4
2
(n-ng)
,{n,-nmax,nmax}]]-
ratio(*EJ/EC*)
2
SparseArray[{Band[{1,2}]1,Band[{2,1}]1},{2nmax+1,2nmax+1}]
已知上述哈密頓量（截斷版本，以
n
g
為自變數，求其本徵值）：
In[]:=
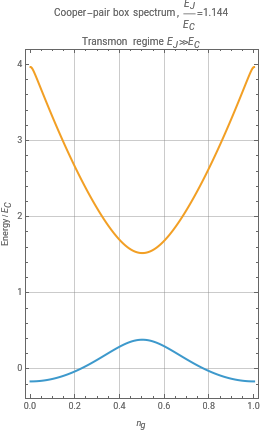
Manipulate​​levelCurves=Table[Sort@Eigenvalues[hamiltonian[ratio,ng0]],{ng0,ngRange=Range[0,1,0.001]}];​​ngEigenval=Transpose[{ngRange,#}]&/@Transpose[levelCurves];​​label=If[ratio<=1,"\nCharge-qubit (CPB) regime
E
J
≪
E
C
","\nTransmon regime
E
J
≫
E
C
"];​​​​RowListLinePlotngEigenval[[;;10,All]],PlotRange->{{0,1},All},PlotLegends->Table[Subscript["E",ToString[j]],{j,10}],Frame->True,FrameLabel->{"
n
g
","Energy /
E
C
"},PlotLabel->"Cooper-pair box spectrum,
E
J
E
C
="<>ToString[ratio]<>label,AspectRatio->1.5,ImageSize->Medium,GridLines->Automatic,BaseStyle->13,ListLinePlotngEigenval[[;;2,All]],PlotRange->All,PlotLegends->Table[Subscript["E",ToString[j]],{j,10}],Frame->True,FrameLabel->{"
n
g
","Energy /
E
C
"},PlotLabel->"Cooper-pair box spectrum,
E
J
E
C
="<>ToString[ratio]<>label,AspectRatio->1.5,ImageSize->Medium,GridLines->Automatic,BaseStyle->13​​​​,{{ratio,0.001,"
E
J
/
E
C
"},.001,20,.001},SaveDefinitions:>True
In[]:=
​
E
J

E
C
E
1
E
2
E
3
E
4
E
5
E
6
E
7
E
8
E
9
E
10
E
1
E
2
能階彎曲與避免交叉現象反映了 Josephson 耦合，這直接證明了電路中能階量子化（這是得獎者研究工作的關鍵部分）。

宏觀量子穿隧（雙能井的二能級模型）

超導電路可以在相位或通量中實現有效的雙井勢，承載局域分別在左、右井且在宏觀上可區分的態。若僅考慮能量最低的兩個局域態，則可建立一個極簡模型，其包含混合兩個井的穿隧耦合，以及可調整的偏壓來傾斜其相對能量。如果將系統準備於其中一個井內，族群會以耦合與偏壓共同決定的頻率在兩個井間產生相干振盪，且在對稱時振幅最大，偏壓增加時振幅減小。純退相干會抑制振盪對比度，能量弛豫則使系統趨向於能量較低井的穩態族群，而有限溫度則會重新填充高能級； 觀察到的相干時間同時反映了弛豫與退相干的影響。時間域振盪、對近對稱時偏壓依賴分裂的光譜學，以及從高溫時的熱激發跨越到低溫時溫度無關的量子穿隧的逸出率或切換電流測量，共同構成這種宏觀量子行為的實驗指紋。
讓我們用哈密頓
H=
ϵ
2
σ
z
+
Δ
2
σ
x
來定義一個二能級系統：
In[]:=
$Assumptions={ϵ,Δ}>0;​​h=
ϵ
2
PauliMatrix[3]+
Δ
2
PauliMatrix[2];​​h//MatrixForm
Out[]//MatrixForm=
ϵ
2
-
Δ
2
Δ
2
-
ϵ
2
這裏 ϵ 表示井之間的偏壓（傾斜），而 Δ 則是隧道分裂。
求此哈密頓的特徵值：
In[]:=
{
ℰ
1
,
ℰ
2
}=Eigenvalues[h]
Out[]=
-
1
2
2
Δ
+
2
ϵ
,
1
2
2
Δ
+
2
ϵ

由上述結果，
Ω=
2
Δ
+
2
ϵ
通常被稱為本徵頻率。
In[]:=
{
e
1
,
e
2
}=Normalize/@Eigenvectors[h]
Out[]=

-ϵ+
2
Δ
+
2
ϵ

Δ
1+
2
Abs
-ϵ+
2
Δ
+
2
ϵ
Δ

,
1
1+
2
Abs
-ϵ+
2
Δ
+
2
ϵ
Δ

,-
ϵ+
2
Δ
+
2
ϵ

Δ
1+
2
Abs
ϵ+
2
Δ
+
2
ϵ
Δ

,
1
1+
2
Abs
ϵ+
2
Δ
+
2
ϵ
Δ


將初始狀態設置在其中一個井的底部（即為
σ
z
的本徵態）:
In[]:=
ψ
0
={1,0};
利用薛丁格方程，在給定時間找到最終態：
In[]:=
ψ[t_]=
2
∑
i=1
Exp[-I
ℰ
i
t]
e
i
.
ψ
0
e
i
//FullSimplify
Out[]=
Cos
1
2
t
2
Δ
+
2
ϵ
-
ϵSin
1
2
t
2
Δ
+
2
ϵ

2
Δ
+
2
ϵ
,
ΔSin
1
2
t
2
Δ
+
2
ϵ

2
Δ
+
2
ϵ

計算穿隧的機率：
In[]:=
{0,1}.ψ[t]{0,1}.ψ[t]//FullSimplify
Out[]=
2
Δ
2
Sin
1
2
t
2
Δ
+
2
ϵ

2
Δ
+
2
ϵ
上述行為假設為相干穿隧，也就是沒有雜訊。實際上，環境交互作用會引入去相干、弛豫以及其他通道，因此動力學會偏離薛丁格方程，而量子位元也會成為一個開放系統。針對這種開放系統動力學，一個常見的模型是林德布拉德主方程：
∂
t
ρ=-[H,ρ]+
∑
k
[
L
k
][ρ]
with
[
L
k
][ρ]=
L
k
ρ
†
L
k
-
1
2

†
L
k
L
k
,ρ
∂
t
ρ=-[H,ρ]+
∑
k
[
L
k
][ρ]
，其中
[
L
k
][ρ]=
L
k
ρ
†
L
k
-
1
2

†
L
k
L
k
,ρ
對應於
L
k
的 林德布拉德/跳躍算符。
定義林德布拉德項：
對於能量弛豫（向下躍遷）的情況，我們有：
對於純退相干（僅相位隨機化而無能量交換）的情況，可以得到：
請注意，從布洛赫波向量在笛卡兒座標系與球坐標系之間的轉換：
求密度矩陣：
定義弛豫的跳躍算符：
將弛豫與純退相結合到動力學方程中：
已知密度矩陣的演化，求布洛赫波向量的演化：
設定動力方程式及初始條件：
將它們全部放入一組參數微分方程：
針對不同參數值，視覺化這些參數微分方程：

引用此筆記本

2025 年諾貝爾物理學獎：宏觀量子效應與量子電腦的曙光​
本篇文章是使用大型語言模型(#LLM)工具所創建的 #繁體中文譯本
作者：Mohammad Bahrami​
原文出自 Wolfram 社群文章：Nobel Prize in Physics 2025: Macroscopic Quantum Effects and the Dawn of Quantum Computer​
Wolfram 社群精選推薦，2025 年 10 月 8 日